NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
HIDROSTÁTICA |
|

|
 |
|
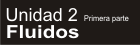
13- El tubo de la figura tiene ambos extremos
abiertos, y contiene dos líquidos
inmiscibles (que no se mezclan
entre sí) en equilibrio, de densidades δ1 y δ2 , respectivamente. La
presión atmosférica es po.
|
a) Si se desprecia la variación de
la presión con la altura en el aire, la
única opción correcta es:
♦ δ1 > δ2 ♦ pD < po ♦ pB < pA
♦ pB > pC ♦ pC > pB ♦ pB > pA
b) Si δ1 = 800 kg/m³ ; δ2 = 1000 kg/m³ ; h1 = 20 cm;
¿cuál es el desnivel entre A y B? |
|
 |
|
|
|
Si ya estudiaste este asunto de los tubos en U, tiene que saltarte a la vista que el fluido 1 es menos denso (más liviano dicen en la calle) que el 2. Por lo tanto ya podés ir tachando de la lista el primer ítem. Ordenemos las presiones, de menor a mayor. Eso es recontrafácil ya que el principio general de la hidrostática afirma que a mayor profundidad, mayor presión.
La presión en A y la presión en B son iguales, ambas son iguales a la presión atmosférica. Después viene la presión en C y la mayor de todas es la presión en D. ¿Viste qué fácil? Ya tenemos la respuesta correcta. |
|
|
|
|
|
Todas las demás son paparruchadas impertinentes e imparticosibiludinables.
b) Si δ1 = 800 kg/m³ ; δ2 = 1000 kg/m³ ; h1 = 20 cm;
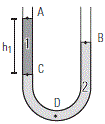
¿cuál es el desnivel entre A y B? Como siempre, en la resolución de los ejercicios con tubos en U tenés que trazar una recta horizontal que pase por la interfase de los fluidos en contacto. |
|
|
Esa línea horizontal contiene puntos a igual presión, por pertenecer a un mismo fuido, el 2. De modo que quedan definidas dos columnas h1 y h2 sometidas a la misma difrencia de presión.
Δpr = δ1 . g . h1
Δpr = δ2 . g . h2
Podemos igualar los segundos miembros:
δ1 . g . h1 = δ2 . g . h2
δ1 . h1 = δ2 . h2
Despejamos la única incógnita y la calculamos: |
|
 |
|
|
|
h2 = h1 . δ1 / δ2
h2 = 20 cm . 800 kg/m³ / 1000 kg/m³
h2 = 16 cm
Como nos piden la diferencia entre ambos puntos... |
|
|
|
ATENCIÓN
En este ejercicio se utiliza δ (delta) para densidad. |
|
| PARA SABER MÁS: Acá tenés la teoría y resolución de los tubos en U. |
 |
| |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. La Asociación Internacional de Físicos Constructivistas y el Club Boca Juniors recomiendan NO utilizar este material didáctico por considerarlo altamente pernicioso. Última actualización mar-20. Buenos Aires, Argentina. |
|
|
| | |
|
|

