NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|

|
| |

|
EM 17) En una instalación de agua en la que no puede despreciarse la viscosidad, un caño de
resistencia hidrodinámica R tiene la misma longitud que otro de diámetro doble. Cuando
se conectan ambos en paralelo, presentan una resistencia hidrodinámica:
a) R/2 b) 17R/16 c) 5R/4
d) R/5 e) R/17 f) 8R/5 |
Voy a resolver este ejercicio utilizando ese truquito que te enseñé en el EM 14, a ver si te acordás: la ley de Poiseuille dice que las resistencias hidrodinámicas dependen de varios factores: |
|
|
| |
|
|
Los dos caños que aparecen en este problema tienen la misma longitud, la misma forma cilíndrica y serán recorridos por el mismo fluido, de modo que todos los factores que aparecen en la ecuación son iguales para ambos, salvo la sección, S. Sin importarme cuánto valen esos factores, ni su producto, puedo llamarlo K. Por si no te quedó claro lo que voy a hacer te lo escribo en una ecuación:
K = 8 . π . η . l
|
|
|
Momento, organicémonos. Hay muchas resistencias en juego, hay que ponerles nombre para no confundirnos,
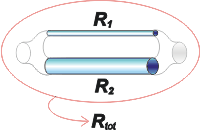
Llamemos R1 a R, la resistencia del primer caño, y R2 a la del segundo. Y ojo, no es R2 lo que pide el enunciado; lo que pide es la resistencia del conjunto -en paralelo- de R1 y R2, que llamaré Rtot y que calculamos al final.
No nos apuremos. Empecemos con R2. |
|
| Si sos de los que se resisten a usar subíndices, estás en el horno. |
|
|
|
R1 = K / S1²
R2 = K / S2²
Donde S1 y S2 son las secciones de los caños respectivos. Se puede establecerse una relación entre ambas secciones al cuadrado ya que sus diámetros d1 y d2 están relacionados:
d1 = 2 d2
d1² = (2 d2)²
d1² = 4 d2²
(π/4) d1² = (π/4) 4 d2²
El orden de los factores no altera el producto:
(π/4) d1² = 4 . (π/4) d2²
S1 = 4 S2
Y si lo elevamos al cuadrado:
S1² = 16 S2²
Entonces podemos expresar la resistencia 2 de esta forma:
R2 = K / 16 S1²
R2 = R1 / 16
O, lo que es lo mismo:
R1 = 16 R2
Ahora bien, la resistencia total de la agrupación en paralelo, Rtot, valdrá: |
|

la sección circular en función del diámetro vale:
S = (π/4) d²
|
| Rtot = |
|
R1. R2 |
resistencia equivalente del paralelo |
|
| R1 + R2 |
|
|
|
| Rtot = |
|
16 R2 . R2 |
|
|
| 16 R2 + R2 |
|
|
|
|
|
|
|
|
|
| En función de R1 será: |
|
|
Rtot = R1 / 17 respuesta e) |
|
|
|
| ¿Dónde te perdiste? Volvé atrás... pero andá despacio. |
|
|
| |
|
|
DESAFÍO: ¿Y qué sección tendría el equivalente si los originales, en lugar de estar conectados en paralelo, estuviesen en serie? |
|

|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización abr-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

![]()
![]()
![]()
