EM 16) Un caño horizontal de 5 cm² de sección, que transporta agua (considerarla fluido ideal) a 2 m/s tiene un tramo de 2,5 cm² de sección. Entonces, la diferencia de presión entre
ambas secciones, expresada en pascales, es:
          a) 500           b) 1,5           c) 6.000
          d) 1.500        e) 375          f) 5

Si consideramos que se trata de un fluido ideal, donde la viscosidad vale cero, entonces podemos pedirle ayuda a nuestro amigo Bernoulli que nos la va a prestar con seguridad.

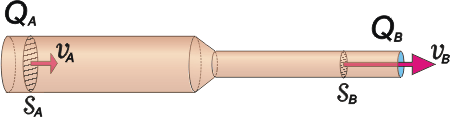
Voy a llamar A a la parte ancha y B a la angosta.           

Los datos que aporta el enunciado permiten afirmar que:

S_A = 2 S_B

Eso tiene su consecuencia en la velocidad, y en la velocidad al cuadrado, ya que el principio de continuidad afirma que:

Q_A = Q_B

S_A . v_A = S_B . v_B

2 S_B . v_A = S_B . v_B

2 v_A = v_B

4 v_A² = v_B²

Ahora podemos plantear la ecuación de Bernoulli (sin los términos de energía potencial ya que todo ocurre a la misma altura).

Δpr = ½ ρ (v_A² – v_B²)

Δpr = ½ ρ (v_A² – 4 v_A²) = – ½ ρ 3 v_A²

Δpr = – ½ 1.000 kg/m³ . 3 . 4 m²/s²

DESAFÍO: Si invirtiésemos el sentido del movimiento del agua, ¿qué ocurriría con la diferencia de presión?