NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|

|
| |
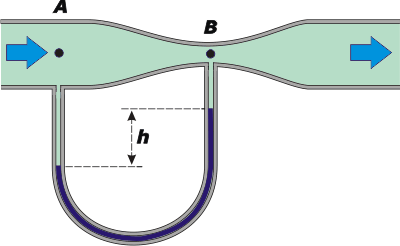
NMS 12 - La cañería representada en la figura tiene una sección transversal A = 36 cm² en la parte ancha y B = 9 cm² en el estrechamiento. En régimen estacionario cada 5 segundos salen de la misma, 27 litros de agua. Calcular:
a) La velocidad en el estrechamiento.
b) La diferencia de presión entre ambas secciones.
c) La diferencia de alturas entre las columnas de mercurio en el tubo en U conectado debajo.
|
|
|
|
¡¡¡Jaaaaa!!! ¡¡¡Al fin apareció!!! ¿Qué cosa? El dispositivo éste. Se llama venturi, o más propiamente: medidor de flujo Venturi. Mirá, más allá de lo que se trate, es algo que podemos resolver sin más conocimientos que los que ya utilizamos. La primera pregunta podemos responderla sencillamente aplicando el principio de continuidad y la descripción cinética del caudal:
Q = QA = QB = 27 L / 5 s = 0,027 m³/ 5 s = 0,0054 m³/s
Hallemos la velocidad en B.
QB = SB . vB
Por lo tanto:
vB = QB / SB
vB = 0,0054 m³/s / 0,0009 m²
|
|
|
| |
|
|
Ya que estamos, averigüemos la velocidad en A.
vA = QA / SA
vA = 0,0054 m³/s / 0,0036 m²
vA = 1,5 m/s
Si consideramos que se trata de un fluido ideal, donde la viscosidad vale cero, entonces podemos pedirle ayuda a nuestro amigo Bernoulli que nos la va a prestar con seguridad.
ΔP = ½ ρH2O (vA² – vB²)
ΔP = ½ 1.000 kg/m³ (36 m²/s² – 2,25 m²/s²)
ΔP = ½ 1.000 kg/m³ 33,75 m²/s²
|
|
|
|
|
|
Esa es la diferencia de presión entre la parte ancha del caño y la angosta. Obviamente es mayor en la parte ancha, donde la velocidad del flujo es menor. Por eso el fluido penetra más en el asa del tubo en U de la parte ancha y menos en el asa de la parte angosta... produciendo una diferencia de altura en el mercurio que descansa en la parte baja del tubo en U.
Fijate que en el tubo en U la situación es estática. Eso nos va a permitir calcular la diferencia de alturas de la columna de mercurio utilizando el principio general de la hidrostática (para hacerlo sencillo voy a despreciar las presiones que ejercen las columnas de agua sobre el mercurio*). Entonces:
ΔP = ρHg . g . h
Donde ρHg es la densidad del mercurio que todo el mundo, desde los 5 años, debe conocer. g es la aceleración de la gravedad. h es la diferencia de alturas que estamos buscando. Y ΔP es la diferencia de presión entre los puntos superiores de las asas del tubo en U. Despejemos h:
h = ΔP / ρHg . g
h = 16.875 Pa / 13.600 kg/m³ . 9,8 m/s²
|
|
| |
|
|
| El medidor de flujo de Venturi permite inferir a partir de una diferencia de altura de fácil visualización, la velocidad del fluido dentro del caño. |
|
|
O sea, el camino inverso de lo que hicimos en este ejercicio. También se lo llama tubo de Venturi. Pero no lo inventó Venturi (Giovanni Battista Venturi, 1746-1822) que sí fue el que se dio cuenta que en el angostamiento de cualquier conducto se produce una baja de presión.
En la actualidad los tubos de Venturi reemplazan el tubo en U con mercurio por un manómetro cuyo display traduce automáticamente la diferencia de presión a la medida de caudal que circula por la cañería. |

|
|
|
|
| |
|
|
*DESAFÍO: Hallar la diferencia de altura de mercurio sin despreciar la presión de las columnas de agua |
|

|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco la colaboración de Fabricio Choque. Última actualización sep-13. Buenos Aires, Argentina. |
|
|
| | |
|
|

![]()
![]()
![]()
