NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|
|
| |
|
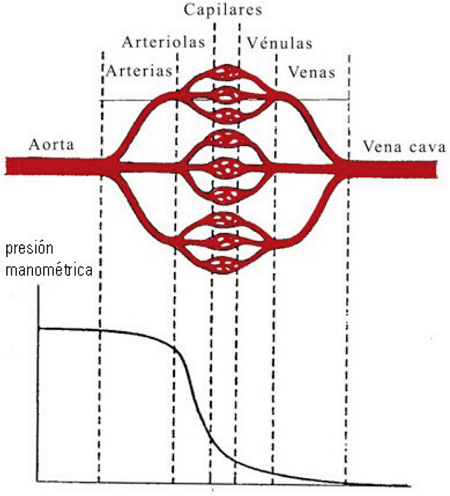
44 - Se presenta un esquema muy simplificado de la circulación sistémica. La sangre sale, a gran presión, impulsada por el corazón a través de la aorta. Tras sucesivas ramificaciones de arterias, arteriolas y capilares irriga a los órganos, músculos y piel. Ese flujo de entrada es colectado por las vénulas y venas que devuelven la sangre al corazón. A lo largo del árbol sanguíneo la sangre va perdiendo presión por efectos viscosos.
|
a) Observe el gráfico cualitativo de la presión manómetrica a lo largo del circuito sanguíneo y analice en qué tramo es mayor la resistencia. |
|
|
 |
|
|
Mirando el gráfico de presión a lo largo del árbol vascular se observa claramente que la caída de presión más abrupta se produce a la altura de las arteriolas.
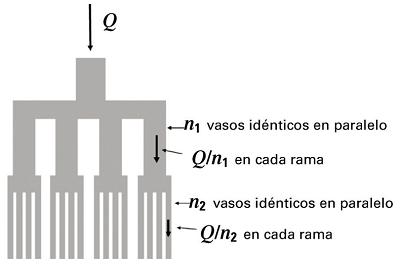
b) El flujo en la aorta (Q = 80 cm3/s) entra en su totalidad en las arterias grandes, luego ese caudal se reparte por entero en las arterias pequeñas y arteriolas; después ese flujo íntegramente entra en los capilares. En cada nivel de flujo podemos modelar el sistema como el de n vasos dispuestos en paralelo de igual grosor y longitud, donde el valor de n es mayor en los sucesivos niveles de flujo.
|
|
|
 |
|
|
| Demuestre que la caída de presión en cada nivel se puede calcular con la expresión: |
|
|
| Δp = |
|
8 η L |
. Q |
|
| n . π . r4 |
|
|
|
Donde L y r son la longitud y el radio de cada rama, n es el número de vasos idénticos en paralelo en el nivel considerado y Q es el caudal total. OK, es sencillo. La pregunta es cuánto val la resistencia total de un conjunto de vasos asociados en paralelo. Y vos lo sabés. Llamemos RT a la resistencia del conjunto y R a la resistencia de un solo vaso que integra el conjunto y que es igual a la de los otros vasos. Entonces: |
|
|
| |
1 |
= |
1 |
+ |
1 |
+ |
1 |
+ ... + |
1 |
|
n sumandos |
|
|
|
|
|
| RT |
R |
R |
R |
R |
|
|
|
En esa suma de fracciones todos los sumandos son identicos, de modo que: |
|
|
|
|
|
| De donde: |
|
|
|
|
|
| Y aplicando la ley de Poiseuille que describe el valor de la resistencia de cada tubo, R, tenemos: |
|
|
|
|
|
| Por útimo, apliquemos la ley de Ohm, Δp = RT . Q, con lo que llegamos: |
|
|
| Δp = |
|
8 η L |
. Q |
|
| n . π . r4 |
|
|
|
| c) Calcule la caída de presión en cada nivel de flujo en este modelo simple confirmando los valores indicados en el cuadro. Considere una viscosidad de la sangre de 4 x 10-3 Pa.s. OK, el cuadro que aporta el enunciado incluye los resultados. Pero vamos a hacer al menos uno de los cálculos porque es muy importante que sepas hacerlo. |
|
|
| |
radio (cm) |
long. (cm) |
n |
Δp (mmHg) |
| aorta |
1,25 |
10 |
1 |
0,025 |
| grandes arterias |
0,2 |
75 |
200 |
1,4 |
| arteriolas |
0,0031 |
0,6 |
5 x 105 |
79 |
| capilares |
0,00035 |
0,2 |
1010 |
8,2 |
|
|
|
Vamos con el de las arteriolas. Hay que homogeneizar las unidades.
η = 4 x 10-3 Pa.s = 3 x 10-5 mmHg.s
|
|
|
| Δp = |
|
8 . 3 x 10-5 mmHg.s . 0,6 cm |
. 80 cm3/s = 79,46 mmHg |
|
| 5 x 105 . π . (0,0031 cm)4 |
|
|
|
Confirmado.
d) El radio de los capilares es casi diez veces menor que el de las arteriolas lo que implicaría que la resistencia en cada fino capilar sea casi 10.000 veces mayor que la de cada arteriola (¿por qué?), ¿cómo se explica que la mayor caída de presión se dé a nivel de las arteriolas? La respuesta de la guía lo explica claramente: La incidencia de la potencia cuarta en el radio, en el denominador de la ley de Poiseuille, hace que un conducto con un radio 10 veces menor tenga una resistencia hidrodinámica ¡¡¡10.000 veces mayor!!! (104 = 10.000). Sin embargo, lo que debemos considerar es la resistencia equivalente de todo el conjunto, que se obtiene dividiendo la de cada elemento por el número de los mismos. El número de capilares es muchísimo mayor que el de las arteriolas por lo que la resistencia equivalente de estas resulta mayor que la resistencia equivalente de los capilares. |
|
|
| |
|
|
COMENTARIO: El radio de las arteriolas es variable y está comandado por el sistema nervioso central autónomo. Es la llave maestra del sistema vascular. |
|
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jul-22. Buenos Aires, Argentina. |
|
|
| | |
|
|
