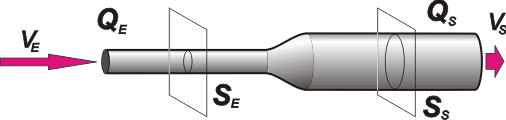
Viscosidad insignificante alude al hecho de que podés considerar a éste un fluido ideal, lo cual te va a permitir comparar esas dos posiciones de la conducción -que llamaré E y S- con el principio de Bernoulli. Pero primero miremos un esquemita.

Escrita como ecuación, la condición del ejercicio dice:

S_S = 3 S_E

Eso tiene su consecuencia en la velocidad, y en la velocidad al cuadrado, ya que:

Q_S = Q_E

S_S . v_S = S_E . v_E

3 S_E . v_S = S_E . v_E

3 v_S = v_E

Y en los cuadrados:

9 v_S² = v_E²

v_S² = v_E² / 9

Ahora podemos plantear la ecuación de Bernoulli (sin los términos de energía potencial ya que todo ocurre a la misma altura) para calcular la diferencia de presión, ΔP.

ΔP = ½ ρ (v_E² – v_S²)

ΔP = ½ ρ (v_E² – v_E²/ 9) = ½ ρ (8/9) v_E²

La nueva condición del ejercicio relaciona los diámetros de los tubos, no sus secciones:

d_S = 3 d_E

d_S² = 9 d_E²

Pero a partir de ello podemos relacionar las secciones (acordate que una sección circular es igual a S = (π/4) d²

(π/4) d_S² = 9 (π/4) d_E²

S_S² = 9 S_E²

Y esto tiene su consecuencia en la velocidad, y en la velocidad al cuadrado, ya que:

Q_S = Q_E

S_S . v_S = S_E . v_E

9 S_E . v_S = S_E . v_E

9 v_S = v_E

81 v_S² = v_E²

v_S² = v_E² / 81

Ahora planteamos la ecuación de Bernoulli:

ΔP = ½ ρ (v_E² – v_S²)

ΔP = ½ ρ (v_E² – v_E²/ 81 ) = ½ ρ (80/81) v_E²

En ambos casos se trata de un aumento de presión ya que en la salida siempre tenemos menor velocidad que en la entrada y, estando a la misma altura, a menor velocidad mayor debe ser la presión.

Para saber más: