NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
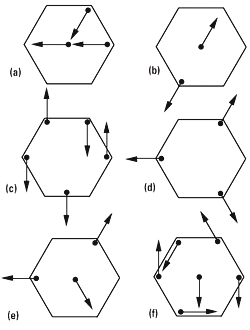
FIS s2.22- Lasfiguras representan cuerpos rígidos
consistemas de fuerzas aplicadas. Todas las fuerzas tienen módulo igual a 1 N. Determine qué sistemas son equilibrados y cuáles no. En es tos últimos, encuentre dos pares de sistemas equivalentes entre sí. En los sistemas que no es tán equilibrados, indique una fuerza equilibrante, si existe.
Si no existe, indique un sistema equilibrante. |
|
 |
|
|
Si no te molesta, vamos despachando los fáciles y dejamos los difíciles para el final.
Arranquemos con el (b). |
|
|
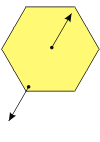 |
Indudablemente el más sencillo. Las dos fuerzas son iguales y opuestas, y actúan sobre la misma recta de acción. El lugar sobre la recta de acción no tiene ninguna relevancia, la propia rigidez del cuerpo lo garantiza. De modo que este cuerpo está en equilibrio traslacional y rotacional.
ΣF = 0 y ΣM = 0
|
|
|
|
Vamos con el (d). |
|
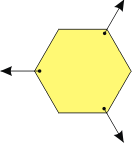 |
Este cuerpo también está en equilibrio traslacional y rotacional. Fijate que las 3 fuerzas son concurrentes (en el centro del cuerpo) de modo que si tomáramos el centro de rotaciones en el centro del cuerpo los 3 momentos serían nulos (y su suma también). En cuanto a lo traslacional también es obvio, pero no tan fácil de explicar. Debido a la gemetría de los hexágonos las fuerzas oblicuas forman 60 grados con la horizontal, de modo que su componente horizontal vale F cos 60° = ½ F. En definitiva dos de estas tiran para la derecha y una entera para la izquierda.
ΣF = 0 y ΣM = 0
|
|
|
| |
| |
| |
| |
| |
| Vamos con el (e). |
|
 |
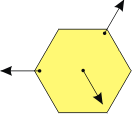 |
Este caso es idéntico al anterior. Ya te aclará que no interesa en qué posición de la recta de acción se aplique una fuerza, mientras las tres fuerzas sean concurrente no habá rotaciones. Y en cuanto a lo traslacional vale exactamente lo mismo que razonamos para el sistema anterior.
ΣF = 0 y ΣM = 0
|
|
|
| Que pase el que sigue, (a). |
|
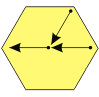 |
Este sistema presenta un claro desequilibrio, hay fuerzas netas hacia la izquierda y hacia abajo que no están equilibradas. Por otro lado las tres fuerzas son concurrentes, de modo que aunque el cuerpo acelere hacia izquierda-abajo... lo hará sin rotaciones.
ΣF ≠ 0 y ΣM = 0
|
|
|
| Ahora se va a poner peludo: |
|
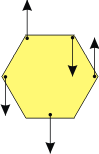 |
Tiene una parte sencilla, la traslacional. 3 fuerzas tiran verticalmente para abajo y solo 2 tiran verticalmente para arriba. O sea, el cuerpo debe acelerar hacia abajo.
En cuanto a lo rotacional no es fácil explicarlo con palabras, pero seguime. Tomemos el centro del hexágono como centro de momentos. La fuerza de abajo, su recta de acción pasa por ese centro o sea, queda descartada. La fuerza de más a la izquierda hace girar en sentido antihorario, y la de más a la derecha también y ambas se halla a un radio del hexágono. Las dos fuerzas el el lado superior provocan giro en sentido horario pero se hallan del centro a una distancia (sus rectas de acción) de medio lado. Como medio lado es menor que un radio, las fuerzas que provocan giro antihorario le ganan a las que provocan giro horario. Entonces el cuerpo girará en sentido antihorario.
ΣF ≠ 0 y ΣM ≠ 0
|
|
|
Vamos con el último (mamita salvame), el (f). |
|
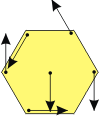 |
No le encuentro otra manera de resolverlo que poniéndole nombre a cada fuerza y plantear las ecuaciones. Hacelo vos, yo te guío: tomá centro de rotaciones al centro del hexágono. De cada fuerza prestale atención a su recta de acción. La distancia al centro siempre vale 1 radio o una apotema (la distancia entre el centro y el punto medio de un lado), por ejemplo la fuerzas de más a la derecha está distanciada un radio, las dos fuerzas de más arriba distanciadas una apotema.
Si trabajás bien tenés que llegar a:
ΣF ≠ 0 y ΣM ≠ 0
|
|
|
| DESAFIO: ¿Cuánto vale la apotema, a, de un hexágono en función del radio, R? |
|
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina.
|
|
|

