NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática del cuerpo extenso
|
|

|
| |
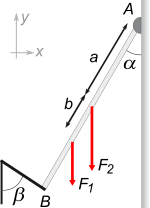
FIS s2.17 - Una varilla homogénea de 40 cm de longitud y de peso despreciable se encuentra en equilibrio sostenida en un extremo (A) por una articulación y el otro extremo (B) por una soga inextensible. Sobre la varilla actúan las fuerzas verticales F1 y F2, según muestra la figura.
Siendo α = 30º, β = 60º, a = 20 cm, b = 4 cm, F1 = 5 kgf y F2 = 10 kgf.
Calcular, expresándolas verctorialmente:
a) la fuerza que ejerce la soga sobre la varilla.
b) la fuerza que hace la articulación en A sobre la varilla. |
 |
|
|
Sin duda alguna, todo empieza con el DCL. |
|
|
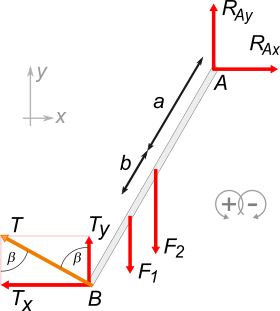 |
Las fuerzas que actúan sobre la escalera son cuatro: las dos verticales indicadas por el enunciado F1 y F2, la de la articulación A (que ya represento descompuesta en RAx y RAy y la tensión que ejerce la saoga que también descompuse en Tx y Ty.
Conviene que ya te fijes que entre las componentes de la tensión existe un compromiso geométrico:
Tx = T sen β
Ty = T cos β
Bien, podemos plantear las ecuaciones de equilibrio:
|
|
|
ΣFx = RAx — Tx = 0
ΣFy = RAy + Ty — F1 — F2 = 0
Tomemos el centro de momentos en A.
ΣMA = F2 a sen α + F1 (a+b) sen α — Tx L cos α — Ty L sen α = 0
Esta ecuación de suma de momentos la podríamos pantear de este otro modo mucho más sencillo. Para hacerlo bastaba con que te dieras cuenta de que el ángulo entre la varilla y la soga vale 90º (α + β), acá te lo aclaro: |
|
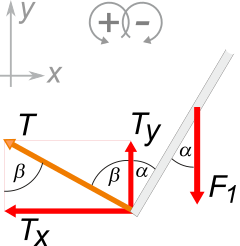 |
En este esquema podés visualizar con claridad quién es α y cuál es su relación con β, el par de ángulos aportados por el esquema del enunciado.
Los ángulos α y β valen 30 y 60 grados respectivamente. De modo que su suma vale 90º, lo que equivale a decir que entre la soga y la varilla se forma un ángulo recto, 90º. Esto nos permite plantear la sumatoria de momentos de un modo más sencillo (totalmente equivalente al anterior). |
|
|
ΣMA = F2 a sen α + F1 (a+b) sen α — T . L = 0
De ahí podemos despejar la fuerza que ejerce la soga:
T = ( F2 a sen α + F1 (a+b) sen α ) / L
T = ( 10 kgf . 20 cm . 0,5 + 5 kgf . 24 cm . 0,5) / 40 cm
T = 4 kgf
Como el enunciado pide expresarla vectorialmente, la descomponemos según su expresión (mirá allá arriba): |
|
| |
T = — 3,464 kgf î + 2 kgf ĵ |
|
|
|
Y con las ecuaciones de Newton sale el valor de la reacción en A: |
|
|
| |
RA = 3,464 kgf î + 13 kgf ĵ |
|
|
|
|
|
|
|
Desafio: ¿módulo de R y dirección de cada fuerza? |
|
 |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-19. Buenos Aires, Argentina. |
|
|
|

