NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
FIS s2.04 - Dónde habrá que colocar un apoyo fijo en
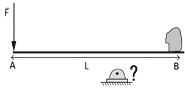
la tabla para usarla a modo de palanca si se desea mantener en equilibrio una piedra de peso 225 kgf ubicada en el extremo B, aplicando una fuerza de 25 kgf en el extremo A. La longitud de
la tabla es de 2 m y el peso despreciable.
a- La tabla está horizontal.
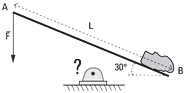
b- La tabla está inclinada 30°. |
 |
 |
|
| Mantener en equilibrio significa que la sumatoria de las fuerzas sobre la tabla vale cero y que la sumatoria de momentos también vale cero. En este ejercicio alcanza y sobra con la ecuación de momentos. |
|
|
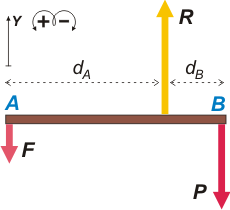 |
Tomemos como punto de referencia de los momentos el punto de apoyo, O, cuya posición queremos averiguar (eso nos permite prescindir de la fuerza en el apoyo, R). Según nuestra convención de signos...
ΣMO = F. dA — P. dB = 0
De donde:
F . dA = P . dB
Pero además sabemos que:
dA + dB = L
|
|
| Mientras no apeles a la operatoria producto vectorial, el orden de los factores en la definición de momento es indistinto |
|
No hace falta que te explique por qué. De ésta despejemos dB y lo que nos dé lo metemos en la anterior.
dB = L — dA
F . dA = P . (L — dA)
Ahora despejamos dA y ya.
F . dA = P . L — P . dA
F . dA + P . dA = P . L
dA = P . L / (F + P)
dA = 225 kgf . 2 m / (25 kgf + 225 kgf)
|
|
| |
dA = 1,8 m |
(desde el extremo A) |
|
|
| Vamos a la parte b). |
|
|
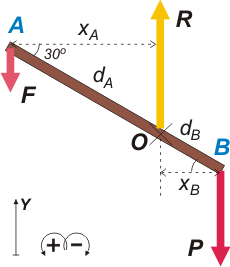 |
La misma barra, las mismas fuerzas... lo único que cambia son las distancias entre lal fuerzas y el punto de referencia (o centro de momentos, O), ya que esas distancias son en realidad la menor distancia entre el centro y la recta de acción de las fuerzas. Acá las llamé xA y xB. Ahora bien, si mirás los triangulitos que quedaron formados con la tabla coincidirás conmigo en que:
xA = dA cos 30°
xB = dB cos 30°
OK, ahora reahagamos el planteo: |
|
|
|
ΣMO = F. xA — P. xB = 0
De donde:
F . xA = P . xB
O lo que es lo mismo:
F . dA cos 30° = P . dB cos 30°
F . dA = P . dB
¡Epa!, tenemos lo mismo que antes. No digamos una palabra más: |
|
 |
| |
dA = 1,8 m |
(desde el extremo A) |
|
|
| Desafio: ¿Cómo se llamaba la relación entre los ángulos que forma la barra con la horizontal en A y en B? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
|

