NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
FIS s2.03- Un cuadrado tiene 0,6 m de lado. A lo largo
de sus lados actúan fuerzas de 1,36 kgf;
1,82 kgf; 2,72 kgf y 5,45 kgf respectivamente. Calcular el momento total:
a) Con respecto al centro del cuadrado O.
b) Con respecto al punto A (ver figura)
c) Si se quiere mantener el cuadrado en equilibrio
aplicando una única fuerza, en cada uno de
los casos anteriores: ¿cuál sería su módulo,
dirección y sentido?, ¿dónde se aplicaría? |
|
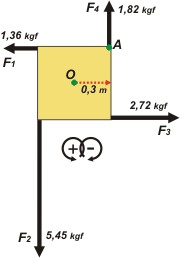 |
Espero que nadie se enoje, pero modifiqué un poquito el dibujo original del ejercicio: dibujé las fuerzas en escala. Y para resolver el problema le puse nombre a las fuerzas, porque... como vos ya sabés le tengo un poco de alergia a los números.
Fijate que la distancia entre la recta de acción de cada fuerza y el punto O, que está en el centro del cuadrado es la misma para todos, la voy a llamar d, y vale 0,3 m, o sea, la mitad del lado. Respecto de O, todas rotan en sentido antihorario,
ΣMO = F1 . d + F2 . d + F3 . d + F4 . d = |
|
|
|
|
Ahora vamos a hacer lo mismo pero considerando las distancias de las rectas de acción de cada fuerza con el punto A. Vale cero para las fuerzas F1 y F4, ya que sus rectas de acción contienen a A. Las otras dos pasa a un lado (0,6 m) de distancia, que voy a llamar L (por lado). Vuelven a girar en el mismo sentido (positivo).
ΣMA = F2 . L + F3 . L =
|
|
|
|
| O sea que el momento de un conjunto de fuerzas (o la sumatoria de momentos) suele ser un valor relativo, que depende del punto desde el que se considere la rotación posible. Y digo suele porque no siempre es así. Por ejemplo, si las cuatro fuerzas fuesen iguales, supongamos 2,74 kgf, la suma de momentos valdría lo mismo tomando el punto O, o el A como centro. Probalo. |
|
 |
| DESAFIO: Esa particular invariancia todavía se cumple con un sistema mucho más sencillo, llamado par de fuerzas o cupla, que consiste en dos fuerzas paralelas, de igual módulo, signo contrario y sus rectas de acción distanciadas. Te propongo hacer una demostración general y te pongo como ejemplo un sistema muy parecido al del ejercicio que ya hicimos. |
|
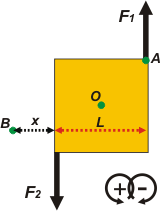 |
La propuesta consiste en hallar el momento de la cupla (o sea la sumatoria de las fuerzas que están actuando en este ejercicio) considerando tres centros de momento distintos: A, O y B, siendo L el lado del resctángulo y estado B a una distancia desconocida x del rectángulo.
F1 = F2 y F1 ll F2
Si operás bien los tres resultados deben ser iguales, el momento de la cupla, MC, será:
MC = F1 . L = F2 . L
o sea el valor de una sola de las fuerzas que integran la cupla por la distancia entre las rectas. |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Ignacio Lobato por el envío de una errata. Última actualización ene-07. Buenos Aires, Argentina. |
|
|
|

