 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
NMS s2.20 - Demostrar que el momento de una fuerza es igual a la suma de los momentos de las componentes de esa fuerza según cualquier sistema de referencia. |
|
| Espero que te guste este ejercicio, se me ocurrió dando clase un día que tuve que plantear la diyuntiva entre considerar el momento de una fuerza o la suma de los momentos de sus componentes, sin tiempo para intentar una demostración. Es lo que los físicos suelen llamar ejercicio teórico, que son inusuales en No me salen. |
|
|
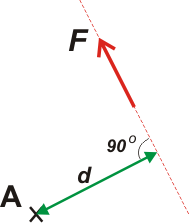 |
Supongamos una fuerza cualquiera, F, y un punto cualquiera A que tomaremos como centro de momento.
Una forma de pantear el momento de F respecto a A (mi modo preferido) es prolongar la recta de acción de F y trazar el segmento perpendicular a esa recta que contiene a A. Esa es la distancia que interesa para hallar el momento.
AMF = F . d
Te vuelvo a aclarar que no hay uniformidad de criterio en el símbolo para momento. |
|
|
| Cualquier posición de la fuerza F sobre su recta de acción es indistinta y no cambia su momento respecto de A, de modo que si no te molesta, y sólo a los fines de la simplicidad de esta demostración, voy a colocar la fuerza F en una posición más amable: |
|
| |
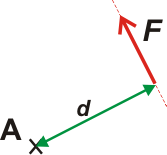 |
F tiende a provocar un giro de sentido anti-horario respecto a A. Tomemos ese sentido como positivo. |
|
|
|
Ahora elijamos un sistema de referencia de ejes x e y que no coincida con ninguna de las derecciones implicadas hasta ahora. |
|
|
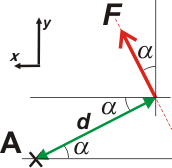 |
El que puse forma un ángulo arbitrario α con la dirección de d, que vuelve a repetirse con F.
Antes de continuar conviene que te cerciores de que los tres ángulos que indiqué, los tres son idénticos y amerita que les ponga el mismo nombre, α. Te doy una ayuda:
(Los dos de abajo por alternos internos entre paralelas, y con el de arriba son comprendidos entre antiparalelas). |
|
|
|
| Ahora reemplacemos la fuerza F por sus componentes (o proyecciones) según el sistema de referencia elegido. |
|
|
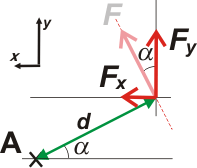 |
Acá viene el planteo primordial de este ejercicio: lo que queremos demostrar es que el momento de F es igual a la suma de los momentos de sus componentes. En símbolos:
AMF = AMFy + AMFx
Me gustaría que antes de continuar te cerciores de que ambas componentes tienden a producir -respecto de A- el mismo sentido de giro que F (anti-horario), con lo cual podemos quedarnos tranquilos y desentendernos de los asuntos de signo. |
|
|
|
Escrita un poco más desarrollada, la igualdad que queremos demostrar es ésta:
F . d = Fy . dFy + Fx . dFx
Veamos a qué son iguales los momentos de cada componente, ya que tanto las componentes se relacionan con F como las distancias se relacionan con d: |
|
|
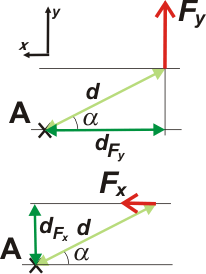 |
Fy = F cos α
Fx = F sen α
Por otro lado las distancias te las represento en este nuevo gráfico (utilizando el mismo criterio que al inicio) para que puedas chequear las relaciones que te presento a continuación:
dFy = d cos α
dFx = d sen α
Ahora podemos reemplazar estas igualdades en la igualdad que queremos demostrar: |
|
|
|
F . d = F cos α . d cos α + F sen α . d sen α
F . d = F . d . cos² α + F . d . sen² α
Sacamos F . d como factor común en los términos del segundo miembro:
F . d = F . d . (cos² α + sen² α)
El paréntesis vale 1 sea cual sea α, (se llama relación pitagórica y es muy fácil de demostrar partiendo del teorema de Pitágoras) de modo que podemos prescindir de él, con lo que llegamos a la demostración buscada. |
|
|
|
|
|
| NOTA: si se te atragantó la relación pitagórica y no tenés ganas de demostrarla (es tan sencilla que se puede hacer mentalmente) al menos tomá tu calculadora, elegí arbitrariamente un ángulo cualquiera y planteá esa suma para verificar que da 1. |
|
|
| |
|
|
| DESAFIO: ¿Ocurrirá lo mismo en un sistema de 3 dimensiones? |
|
 |
Algunos los derechos reservados (usted ya seba cuáles).
Se permite su reproducción citando la fuente. Última actualización nov-19. Buenos Aires, Argentina.
|
|
|

