NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
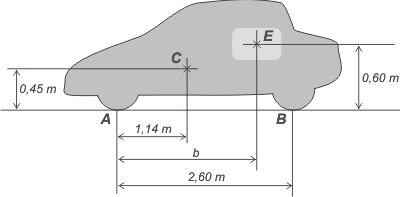
| NMS s2.16* - Con el motor retirado, la masa del automóvil es de 1.100 kg y su centro de gravedad está en C. (a) Se quiere situar el motor de 220 kg cuyo centro de gravedad denominamos E, de manera que el centro de gravedad del conjunto quede a mitad de distancia entre las ruedas delanteras, A, y traseras, B. ¿Qué valor debe tener b? (b) Si el automóvil se estaciona sobre una pendiente de subida de 15º ¿qué valor tiene la fuerza de apoyo sobre las ruedas? |
 |
|
Te habrás dado cuenta de que no se esmeraron mucho con el diseño... porque un auto que tiene el motor en esa posición más que un auto es un adefecio. Pero no importa, en lo que hace a la estática es un ejercicio bastante sencillo.
La primera pregunta es muy simple: dónde hay que colocar (horizontalmente) el motor para que el centro de gravedad del conjunto quede a 1,3 m de A, o sea, en el centro de la superficie de apoyo.
La ecuación del centro de masa (el promedio ponderado) es:
(mC + mE) xG = mC xC + mE xE
Donde mC es la masa del auto sin motor, mE es la masa del motor, xG es la posición (horizontal) del centro de masa, xC es la posición del centro de masa del auto sin motor, y xE es la posición del centro de masa del motor.
Si tomamos origen de coordenadas en A, xG vale 1,3 m, xC vale 1,14 m, y xE es nuestra incógnita b. Entonces despejamos xE:
xE = (mC + mE) xG — mC xC / mE
b = ( 1.320 kg . 1,3 m — 1.100 kg . 1,14 m ) /220 kg
|
|
|
|
|
Colocando el motor en esa posición, cada rueda va a soportar la misma fuerza, algo que -en realidad- a los fabricantes de autos no les preocupa demasiado.
Ya que estamos averiguemos cuál es la altura del centro de masa del conjunto (dato que necesitaremos para resolver la segunda parte del ejercicio).
yG = (mC yC + mE yE ) / mC + mE
yG = (1.100 kg . 0,45 m + 220 kg . 0,60 m) /1.320 kg
yG = 0,475 m
Ahora sí, vamos a la segunda parte.
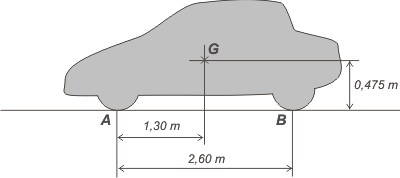
Lo primero que vamos a hacer es aclarar cómo queda el auto armado, según las condiciones que nos pusieron en el ítem anterior. Acá va un esquema: |
|
| |
|
|
|
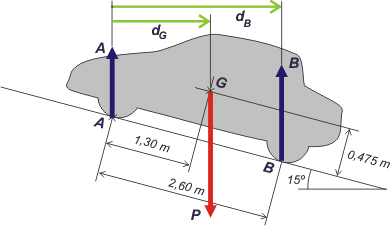
| Ahora inclinamos 15º el auto (mirando hacia arriba) y mostramos las fuerzas que actúan cuando queda así apoyado. |
|
|
 |
|
| Las reacciones en las ruedas no son normales a la pendiente. Con el auto estacionado (como indica el enunciado) tienen una componente paralela al pavimento: el rozamiento. |
|
Se ve que las ruedas traseras van a tener que hacer más fuerza que las delanteras... pero ¿cuánto?
Conocemos el valor del peso del conjunto, P, que vale 1.320 kgf, y queremos conocer el valor de las reacciones en las ruedas A y B. Vamos a aplicar el equilibrio de momentos, pero necesitamos conocer las distancias dG y dB entre las rectas de aplicación de las fuerzas. Se trata de problemas geométricos bastante arduos, pero sencillos. Yo te hago uno solo, y vos hacés el otro sin ayuda. |
|
|
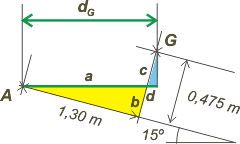 |
Mirá los dos triangulitos rectángulos celeste y amarillo. son semejantes los ángulos A y G valen 15º. Una de las distancias que buscamos, dG, es la suma de los lados a y b. Veamos qué cosas podemos saber:
dG = a + d y 0,475 m = b + c |
|
|
|
a = 1,30 m / cos 15º = 1,346 m
b = 1,30 m . tg 15º = 0,348 m
c = 0,475 m — b = 0,127 m
d = c . sen 15º = 0,033 m
De donde:
dG = 1,379 m
Si te tomás el trabajo, encontrarás que:
dB = 2,511 m
Ahora aplicamos el equilibrio de momentos:
ΣMA = 0 → P . 1,379 m = B . 2,511 m
De donde:
B = 725 kgf
El apoyo en las delanteras sale por diferencia, ya que la suma de los apoyos debe ser igual al peso. |
|
|
| |
B = 725 kgf y A = 595 kgf |
|
|
|
|
| |
|
|
| * Tomado de Estática, Anthony Bedford, Wallace Fowler, Pearson Educación. |
|
 |
| DESAFIO: La resolución contiene un error conceptual, ¿cuál es? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización sep-13. Buenos Aires, Argentina. |
|
|
|

