NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
| NMS s2.15*- Una varilla homogénea de hierro de 60 cm de longitud, se dobla en angulo recto obteniéndose un perfil L de 20 cm por 40 cm. Si se suspende la varilla asi doblada por el vértice, encuentra el ángulo que formará con la vertical el lado que mide 40 cm cuando la varilla se encuentre en equilibrio. |
|
| Este ejercicio es excelente, por su economía de datos, y por las lecciones que puede brindarnos. Acá tenés la varilla. |
|
|
 |
|
| Le metemos un agujerito justo por donde la vamos a doblar, que quedan definidos dos tramos: tramo 1, t1, el largo, y tramo 2, t2, el corto. El tramo largo es dos veces más largo que el corto. t1 = 2 t2. |
|
Como la varilla es homogénea, los pesos de cada tramo son proporcionales a la longitud... de modo que si llamamos P1 y P2 a los pesos de cada tramo, podemos asegurar que P1 = 2 P2.
Y por el mismo motivo, podemos asegurar que los pesos de cada tramo actúan como aplicados a los centros de gravedad de cada tramo, G1 y G2, que, lógicamente, se hallan en los centros geométricos, o sea, justo en la mitad de cada tramo.
Vamos a llamar S -por suspensión- al agujerito por el cual suspendemos la varilla, ahora doblada, que en adelante podemos llamar escuadra.
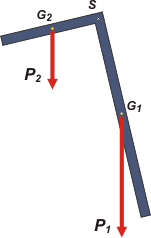
Después de oscilar un rato la escuadra va a alcanzar el equilibrio en una posición como la que te dibujé acá. |
 |
|
|
Y justamente, lo que nos pide el enunciado es que encontremos el ángulo de esa inclinación. Verás que no es muy difícil. |
|
Como en todo equilibrio deben darse dos condiciones: que la suma de todas las fuerzas valga cero. Y que la suma de todos los momentos también valga cero.
La primera condición es trivial, y en este caso no aporta nada a la solución del ejercicio. La segunda es la determinante. Voy a tomar como centro de giros -o momentos- el punto S (qué otro).
ΣMS = 0
MS2 + MS1 + MSS = 0
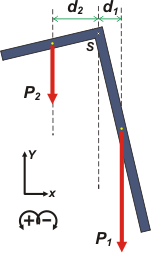
Acordarás conmigo que la fuerza P2 hace rotar la escuadra en forma antihoraria, por lo tanto su momento es positivo. Contrariamente, la fuerza P1 hace rotar la escuadra en forma horaria, por lo tanto su momento es negativo. Por último: el momento de la fuerza de suspensión es cero. Luego, |
 |
|
|
P2 . d2 — P1 . d1 = 0
Recordando la relación entre los pesos de cada tramo, obtenemos:
d2 = 2 d1
El resto es un problema estrictamente geométrico... y bastante sencillo, fijate. |
|
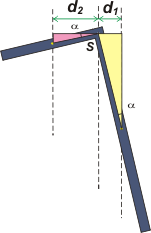
Tracé una recta horizontal por S, y dibujé dos triangulitos que nos van a ayudar. Ambos son rectángulos (espero que te des cuenta de eso)... ¡y semejantes! siendo α el ángulo agudo de los triángulos, que, por otro lado, no es otro que el que nos pide el enunciado del ejercicio.
En el triangulito rosa (el del tramo corto) la hipotenusa es igual a la mitad del tramo corto, ½ t2, y el cateto adyacente a α es d2. Luego:
cos α = d2 /½ t2
En el triangulito amarillo (el del tramo largo) la hipotenusa es la mitad del tramo largo, ½ t1, y el cateto opuesto a α es d1. Luego:
sen α = d1 / ½ t1
|
 |
|
|
|
Si te acordás de que la tangente es igual al seno dividido el coseno, nos queda:
tg α = (d1 / ½ t1) / (d2 /½ t2)
Y recordano que t1 = 2 t2, y que d2 = 2 d1.
tg α = (d1 / ½ 2 t2 ) / (2 d1 /½ t2)
tg α = 1/4
|
|
|
|
|
|
DISCUSION: Como en casi todos los ejercicios de equilibrio de cuerpo extenso, tenés alrededor de un 20% de física y un 80% de álgebra y geometría... pero no es malo que te vayas acostumbrando porque así es la vida.
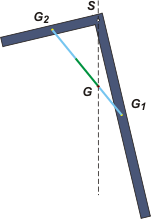
Tampoco hay un único camino para resolver el álgebra, la geometría... ni menos que menos la física, eso ya te lo dije 3.896 veces. De todos los caminos que descarté, me tenté de marcarte éste que sigue: mirá el esquemita que te puse acá.
Cuando un cuerpo cuelga en equilibrio su centro de gravedad, G, ha de hallarse en justo en la vertical del punto de suspensión, S. Y el centro de gravedad debe estar 2 veces más cerca de G1 que de G2, por motivos obvios.
Ahí te aparece más triángulos para jugar y llegar al resultado sin utilizar momentos... en este caso te recomiendo a un tal Thales. |
 |
|
|
|
| |
|
|
| DESAFIO: Resolvé el ejercicio utilizando la propiedad que te acabo de mencionar. |
|
 |
| |
| *Este ejercicio fue tomado -y modificado- de una guía de ejercicios de la UTN de Villa María y me lo suministró gentilmente Claudio Arias (el chumy), a quien se lo agradezco. |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Pablo Nigro por el envío de una errata. Última actualización jul-09. Buenos Aires, Argentina. |
|
|
|

