NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
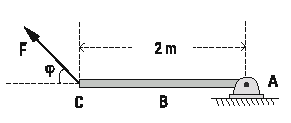
NMS s2.03 - Una barra AC cuyo peso es de 100 N (suponer
que el peso está aplicado en el centro geométrico
de la barrera) se encuentra articulada
mediante una bisagra en el punto A; en el extremo
C se aplica una fuerza F con el objeto de
mantener la barra en equilibrio, horizontalmente.
Calcular:
a- El módulo de la fuerza F sabiendo que φ = 30°.
b- El módulo y dirección (ángulo que forma
con la horizontal) de la fuerza que la bisagra ejerce
sobre la barrera. |
|
 |
|
|
No problem, clásico, fácil, corto, sin lecciones especiales... no sé por qué lo hago.
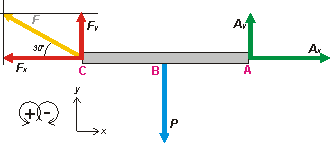
Como siempre, hay que empezar con un DCL. |
|
Supongo que estaremos de acuerdo en que
Fx = F cos φ
Fy = F sen φ
Entonces podemos seguir. |
 |
|
|
Eligiendo como centro de momentos el punto A, y como la barra está en equilibrio tenemos...
ΣFx = 0 → Ax — Fx = 0
ΣFy = 0 → Ay + Fy — P = 0
ΣMA = 0 → P . 1m — Fy . 2m = 0
De la última despejo Fy
Fy = P / 2
entonces ya tenemos F |
|
|
|
Si tenemos F, también tenemos Fx. Eso lo metemos en la primera ecuación, y tenemos Ax. Con la segunda ecuación encontramos Ay. Si queremos el módulo de A, lo hacemos por pitágoras a partir de sus componentes. |
|
|
|
| Y si dividemos Ay / Ax obtenemos la tangente del ángulo que forma A con el eje x |
|
|
|
Ya sé cuál era la lección de este ejercicio. Mostrar que son todos iguales. Todos los ejercicios de estática del cuerpo extenso se resuelven de la misma manera.
a) DCL
b) ΣF = 0 ( ΣFx = 0 y ΣFY = 0 )
c) ΣM = 0 (desde cualquier punto, pero, mejor elegido, menos álgebra)
d) Resolver algebraicamente
e) Gozar de la vida. |
|
| |
 |
| |
| DESAFIO: Resolver nuevamente pero colocar el centro de momentos a una distancia D hacia la derecha de la barra. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

