NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
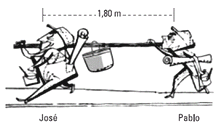
NMS s2.02 - Dos trabajadores Pablo y José transportan
un paquete que pesa 120 kgf, suspendido de una
barra de 2 m de longitud y de peso despreciable,
que llevan a cuestas. ¿En qué posición habrá que
colocar la piedra para que el esfuerzo realizado
por Pablo sea los 2/3 de lo que soportará José? |
 |
|
| No me gusta decirlo, pero entre Pablo y José uno de los dos es un pícaro: Pablo. Pone cara de tonto pero está haciendo un menor esfuerzo. Lo sorprendente es que haga su negocio sin saber lo que es un DCL. |
|
|
 |
No se entiende para qué nos pusieron una barra de 2 m si con una de 1,8 m alcanzaba. Diferente hubiera sido si la barra tenia un peso considerable, pero en este caso... ¡Ah! Ya sé: para que te acostumbres a que en los planteos de los ejercicios puede haber datos sobrantes, o inmecesarios o incluso tontos. Sólo los que saben, superan esa dura prueba.
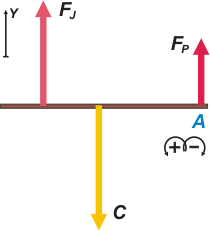
A la fuerza que hace el balde sobre la barra la llamé C (por carga) y las de los operarios las distinguimops por el subíndice. Voy a tomar como centro de giros o momentos el extremo de la barra, A. Desarrollo las dos condiciones de equilibrio: "el cuerpo no se desplaza": Σ Fy = 0 , y "el cuerpo no gira" : Σ MA = 0 |
|
|
|
ΣFy = 0 → FJ + FP — C = 0
ΣMA = 0 → C . d — FJ . 1,80 m = 0
Si contás vas a ver que tenemos 3 incógnitas, con sólo dos ecuaciones. Pero hay un dato del enunciado que todavía no usamos y que si lo sabemos usar lo transformaremos en una tercera ecuación, es el que dice que "el esfuerzo realizado
por Pablo sea los 2/3 de lo que soportará José". Que se traduce así:
FP = FJ . 2/3
Ahora sí, esto está cocinado. Si meto esta última en la primera, me queda
FJ + FJ . 2/3 = C
o lo que es lo mismo
FJ . 5/3 = C
Ahora meto esto en la segunda ecuación, la de momentos, y sale
d . FJ . (5/3) — FJ . 1,80 m = 0
d . FJ . 5/3 = FJ . 1,80 m
d = 1,80 m . 3/5
|
|
|
| |
d = 1,08 m |
(medidos desde Pablo) |
|
|
|
| |
|
|
| DISCUSION: Por qué elegí el punto A para definir los momentos de las fuerzas. La idea es la siguiente: si es dato que el cuerpo (en este caso la barra) está en equilibrio (en este caso no lo dicen explícitamente pero puede entenderse) entonces el cuerpo no gira. Que no gira implica que la suma de todos los momentos de las fuerzas que actúan vale cero... definidos desde cualquier punto. Eso me habilita a elegir arbitrariamente el centro de giro. Habitualmente se elige un centro de giro natural (cuando lo hay) o uno cómodo. Donde cómodo quiere decir que se pueden calcular fácilmente los momentos de las fuerzas que actúan. |
|
 |
| DESAFIO: ¿Cúal sería la posición correcta si la barra pesara 10 kgf ? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

