NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
FIS s1.09 - Calcular qué ángulo máximo pueden formar
con la vertical las cuatro cuerdas de la figura,
para que la fuerza que soporta cada una no
exceda los 500 kgf. (Use consideraciones de simetría). |
 |
|
| Este ejercicio es más fácil de lo que parece. Por suspuesto, como en todo problema de dinámica o estática (que parte de) la principal herramienta es el DCL. Pero hasta llegar a ella vamos a tener que trabajar un poquito. A veces no es sencillo comprender el problema cuando partimos de un esquema en perspectiva. |
|
|
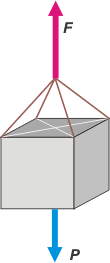 |
Bueno, queda claro que la fuerza que tiene que hacer el guinche para sostener la caja es igual a su peso o sea
F = P = 1.000 kgf
Ahora viene la cuestión. La fuerza del guinche se reparte en cuatro sogas. Supongo que te queda claro que la fuerza que hace cada una NO ES la cuarta parte del peso, no valen 250 kgf cada una, ¿no es cierto?
Claro esas cuatro soguitas no solamente hacen una fuerza vertical (esa sí, sumada da 1.000 kgf) sino que, como están oblicuas, también realizan una fuerza lateral, en conclusión la fuerza que hace cada una es mayor a 250 kgf. Si sos una persona práctica (varón o mujer) entenderás que cuanto más arriba hagas el nudo de separación menos fuerza tienen que hacer tus 4 soguitas, y cuanto más abajo, más cerca de la caja, mayor será esa fuerza. |
|
|
| Ya sabemos varias cosas que la fuerza es mayor que la cuarta parte del peso y que depende del ángulo que forma cada soga con la vertical. Y también sabemos que las cuatro tensiones son iguales. ¿Y cómo sabemos eso? Juastamente a eso se refiere el enunciado cuando te dice que apeles a consideraciones de simetría. Las cuatro sogas tienen idéntica posición respecto de un eje vertical que pasa por el centro de la caja. Si con eso no te cierra, lo lamento, perderás 2 horas de sueño hoy a la noche. |
|
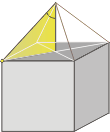 |
Ahora bien, el ángulo que cada soga forma con la vertical podríamos calcularlo a ciegas. Las ecuaciones no te piden que lo visualices. Sin embargo, me resisto a que hagas nada sin entender lo que estás haciendo.
Te puede tocar un problema en el que se pida calcular el ángulo por otros medio y vas frito. Para visualizar el ángulo pensá que la vertical y una soga cualquiera (por ejemplo la delantera izquierda) están en un plano y forman con la caja un triángulo que te dibujé en amarillo. Es rectángulo, aunque por la perspectiva no lo parezca. |
|
|
| Voy a aprovechar esa esquina de la caja para plantear las fuerzas que entran en juego en el ejercicio. |
|
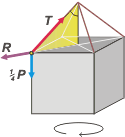 |
Cada soga hace una fuerza máxima que llamaremos T, sobre el vértice de la caja. Ahí también están aplicadas otras dos fuerzas: 1/4 de peso, ¼ P, y la reacción de la caja, R, que no le gusta que la apretujen.
Existe una relación geométrica entre las tres fuerzas, y esa relación tiene que ver con el ángulo del que estuvimos hablando, entre la vertical y la soga. Pero para verlo bien vamos a sacarle la perspectiva, rotándolo un cachito hacia la izquierda hasta que el plano de la diagonal nos quede de frente (en geometría eso se llama rebatir). |
|
|
Por fin apareció el DCL. Ahora vemos claramente el ángulo entre la soga y la vertical, y se ve también que es el mismo que forma la fuerza que hace la soga, T, con su componente vertical. De modo que
Tx = T sen α
Ty = T cos α
Y por fin podemos aplicar la condición de equilibrio
R = Tx
¼ P = Ty
|

|
|
|
La primera ecuación no aporta gran cosa en este ejercicio, pero la segunda sí:
¼ P = T cos α
α = arc cos (¼P/T)
α = arc cos (250 / 500)
|
|
|
|
| |
|
| |
| DISCUSION: Todo el problema no era más que estos últimos 3 renglones, pero poco o nada hubieras aprendido si te los copiaba así, peladitos. |
|
 |
| DESAFIO: En el planteo anterior, ¿cuánto vale la fuerza de resistencia de la caja en cada esquina? ¿Cuánto valdrá la tensión en cada cuerda si el ángulo que forman entre sí, o sea cada una con la de al lado, fuera de 70 grados? ¿Dónde habrá que colocar el nudo para que la fuerza de cada cuerda valga 250 kgf? ¿Qué puede haber dentro de la caja? |
|
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina.
|
|
|

