NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |

|
FIS s1.06- Hallar la tensión en las cuerdas, si el peso
que soportan es de 200 kgf. |
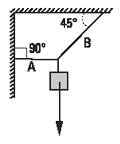 |
Este ejercicio es muy, pero muy sencillo. Y tiene la virtud de mostrarnos un par de conceptos que vamos a tener que incorporar con intensidad, porque los vamos a usar permanentemente.
El primero de ellos es la versatilidad de la 2da. ley de la dinámica, o ley de la masa o ley de Newton. |
|
ΣF = m a
cuando decimos que la sumatoria de todas las fuerzas que actúan sobre un cuerpo es igual al producto entre su masa y su aceleración, no necesariamente tenemos que estar hablando de un cuerpo voluminoso, masivo, regordete. Estamos hablando de casi cualquier cosa que se te ocurra, por ejemplo una molécula, un pedacito de soga, un nudo, un psidegulianoato de merdixongo.
Y cuando hablamos de producto entre masa y aceleración incluímos casos idiotas como que la masa valga cero, o la aceleración valga cero. Tan potente y versátil es esta ley del universo que aún en esas situaciones absurdas resulta útil y eficiente.
En este problema, por ejemplo, nos piden que encontremos los valores de las fuerzas que hacen tres sogas. Qué mejor oportunidad que aplicarle la 2da ley al punto donde se reúnen esas tres fuerzas. El nudito entre las tres sogas. Pero un nudito... ¿qué masa tiene? ¿Qué cuerno es un nudito? NO IMPORTA. Mirá su DCL. |
|
|
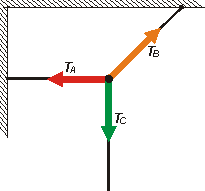 |
Yo dibujé las tres fuerzas con el largo correcto. Eso no tiene mucha importancia. Lo que sí la tiene es que le pongas la dirección, y el sentido correcto, y un nombre razonable.
Fijate que cada soga hace una fuerza en cada extremo y esas fuerzas (que no son par de interacción) son iguales. Para referirme a la fuerza que hace una cuerda puedo prestar atención a cualquiera de los dos extremos. Lo que no puedo hacer es errar el sentido.
Del nudo todas tiran hacia afuera. ¿Te queda claro? |
|
|
| La primera lección fue esa, un nudo es tan apropiado como cualquier otro cuerpo de verdad. La segunda lección viene ahora: habitualmente la gente un poquito experimentada considera a la fuerza que hace la soga de abajo, TC, (por tensión) de este problema como si fuera un dato. Lo cierto es que no lo es. |
|
 |
Es que ya resolvieron mentalmente este problema: Si le plicamos la segunda ley de Newton a ese cuerpo...
ΣF = m a → TC — P = 0
o sea TC = P
que se puede anticipar fácilmente porque el cuerpo está en reposo, su aceleración es cero. Habitualmente hacemos esas cosas. |
|
|
| Y ahora que aprendimos las dos lecciones, resolvamos el problema, que es una pavada. Rehacemos el DCL, pero con todas las fuerzas en sólo dos direcciones. Para eso descomponemos TB |
|
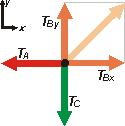 |
ΣFx = m ax
TBx — TA = 0 → TBx = TA
ΣFy = m ay
TBy — TC = 0 → TBy = TC
y no olvides que |
|
|
TBx = TB cos 450 , y TBy = TB sen 450 , y como cos 450 = sen 450 = 0,707 |
|
|
|
|
|
|
|
|
|
| |
|
 |
| DESAFIO: ¿Cuánto valdría TA si el águlo fuese recto? |
|
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina.
|
|
|

