NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
|
 |

|
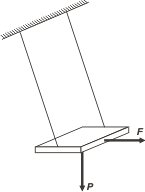
FIS s1.05 - Una persona que pesa 40 kgf se sienta en un columpio cuyos cables podrían romperse con una fuerza de 68 kgf. Calcular la máxima fuerza que podría aplicarse al columpio con una cuerda horizontal sin que lleguen a romperse los cables. |
Como todos los ejercicios de dinámica o estática hay que comenzar por un DCL. Para hacerlo más sencillo voy a "aplastar" la hamaca a lo ancho para quitar la perspectiva que, me parece, complica innecesariamente el ejercicio. |
|
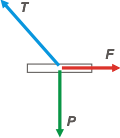 |
Acá lo tenés. Con esta movida que hice, tendremos que tener en cuenta que esa fuerza que representé con T, es la que hacen los dos cables juntos, de modo que el valor máximo que puede hacer T vale 136 kgf (2 por 68).
Las otras dos fuerzas que aparecen son las que menciona explícitamente el enunciado: P que vale 40 kgf, y F, nuestra incógnita. |
|
|
|
| Como ves, las tres fuerzas no son codireccionales (no actúan todas en una única dirección). De modo que tendremos que elegir un sistema de referencia bidimensional (x e y) y reemplazar la o las fuerzas que no coincidan con las direcciones del sistema, por sus componentes. |
|
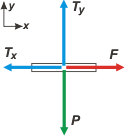 |
Ahora sí, planteamos las ecuaciones de Newton, por separado, para cada eje:
ΣFx = m ax → F — Tx = 0
ΣFy = m ay → Ty — P = 0
La aceleración es nula, ya que para encontrar la fuerza máxima F, debemos hacerlo con la hamaca quieta. Si la aceleración es nula, sus componentes también. Esto es etática. |
|
Si te olvidás de indicar el sistema de referencia te expulsan de la universidad |
| Para expresar el valor de las componentes de T, tenemos que dibujar un triángulo rectángulo en el que aparezca el ángulo de inclinación de las cuerdas, α, y aplicamos un cacho de trigonometría. |
|
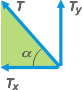 |
Tx = T cos α
Ty = T sen α
Metamos esas igualdades en las ecuaciones de Newton.
T cos α = F
T sen α = P
|
|
|
El resto es álgebra... y bastante sencilla. De la segunda despejamos el seno de α y lo calculamos:
sen α = P / T
sen α = 40 kgf / 136 kgf
sen α = 0,294
Por lo tanto:
α = 17,1°
Con eso vamos a la primera ecuación:
T cos 17,1° = F
136 kgf 0,956 = F
|
|
|
|
| |
|
|
| DESAFIO: ¿Te animás a graficar la variación del ángulo de inclinación de las sogas de la hamaca en función de la fuerza horizontal? |
|
 |
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización sep-14. Buenos Aires, Argentina. |
|
|
|

