NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
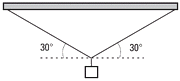
FIS s1.04 - Un objeto de 45,4 kgf de peso está sus pendido mediante dos cuerdas que forman un ángulo
de 30º con un techo hori zontal. Calcular latensión
en cada cuerda. |
 |
|
|
|
|
Un problema tan sencillo... no tiene gracia. Pero me imagino que vos habrás intentado antes y te salió o no te salió, o no habrás intentado, o no me imagino, o tiene gracia... uno nunca sabe...
¿A qué le hacemos el DCL? A la lámpara, claro está. O si querés al nudo superior del que está colgada. Es lo mismo. |
|
|
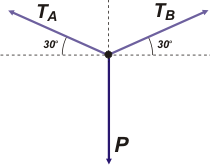 |
Bien, ahí tenés el DCL. Lo hice sobre el nudito superior al objeto. En el que aproveché para ponerle nombre a todas las fuerzas. La soga que hace fuerza hacia abajo (desde el nudo) es igual al peso del objeto... si así no fuera esa soga no estaría en equilibrio. La llamá directamente P (por peso, aunque no es es peso del cuerpo sino que valo lo mismo que él).
Para resolver el ejercicio tenemos que descomponer esas fuerzas, y eso hay que hacerlo en referencia a un sistema de referencia, SR.
|
|
|
|
| Este nuevo DCL es un poco tiene las mismas fuerzas, pero reemplazadas por sus componentes en lo eje x e y. |
|
|
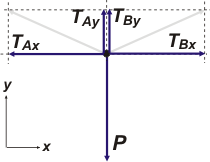 |
En la descomposición vectorial tenemos
TAx = TA cos 30º
TBx = TB cos 30º
TAy = TA sen 30º
TByx = TB sen 30º
|
|
|
|
Ya podemos aplicar la 2da. ley de Newton para los dos ejes.
ΣFx = 0 → TB cos 30º — TA cos 30º = 0
ΣFy = 0 → TB sen 30º + TA sen 30º — P = 0
De la primera ecuación surge que
TB = TA
Si metemos eso en la segunda:
2 TA sen 30º = P
Con lo que podemos calcular el valor de las tensiones:
TA = P / 2 sen 30º
TA = 45,4 kgf / 2 . 0,5
|
|
|
|
|
|
| |
|
|
| DESAFIO: Si se acortan las cuerdas superiores disminuye el ángulo que forman con la horizontal... ¿se pueden acortar tanto que el ángulo llegue a cero? |
|
 |
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se prohibe su utilización sin resolver los desafíos. Última actualización mar-16. Buenos Aires, Argentina.
|
|

