NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
|
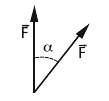
FIS s1.02, a)- En el sistema de la figura, dos fuerzas de
igual módulo forman un ángulo α. Calcular la
equilibrante (módulo, dirección y sentido) si el
ángulo α toma los siguientes valores: |
α = 30º
α = 45º
α = 60º
α = 90º
α = 180º
b) ¿La equilibrante está en el plano formado
por las fuerzas? ¿Por qué? |
 |
| Para hallar la equilibrante, E, podemos hallar la suma o resultante R, luego la equilibrante es la contraria a la resultante: E = - R. |
|
|
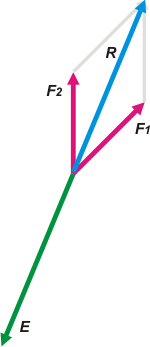 |
Primero resolvámoslo (al menos para el primer ángulo) gráficamente. Porque somos olfas, y qué.
Para sumar las fuerzas F1 y F2 (que dibujé en lila, o rosa, o fuxia... no sé soy hombre), podés dibujar uno a continuación del otro construyendo el paralelogramo. Luego la resultante de ambas fuerzas es su suma, R (que dibujé en celeste).
La equilibrante de R, E (que dibujé en verde), y que es la equilibrante del sistema, es la fuerza opuesta a R. (Vectorialmente: un vector de igual módulo y dirección, pero sentido contrario).
El procedimiento se repite para cada ángulo.
En general no se pretende que hagas cálculos a partir de gráficos, que están más para entender y fijar los conocimientos.
Vamos a la resolución analítica. |
|
|
|
| Para operar analíticamente es imprescindible elegir un sistema de referencia, SR. Cualquiera es igualmente válido, pero casi siempre nos inclinamos por elegir el más cómodo. |
|
|
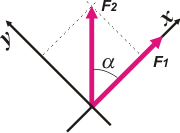 |
Fijate: elegí un SR tal que uno de sus ejes coincida con una de las fuerzas. De esa manera el ángulo que forma
esa fuerza con el eje vale 0º y el que forma la otra fuerza es α.
Como ambas fuerzas son iguales (en módulo) hagamos
|F1|= |F2|= |F2|
|
|
|
|
F1 = |F1| . î
F2 = |F|. cos 30º î + |F|. sen 30º ĵ
Vamos a la suma:
R = (|F| +|F|. cos 30º) î + |F|. sen 30º ĵ
R = |F|. (1+ cos 30º) î + |F|. sen 30º ĵ
Y ahora la equilibrante:
E = — |F|. (1+ cos 30º) î — |F|. sen 30º ĵ
|
|
|
| |
E = — 1,866 |F| î — 0,5 |F| ĵ |
|
|
|
|
Si querés saber el módulo de la Equilibrante:
|E|²= (— 1,866 |F|)² + (0,5 |F|)²
|
|
|
|
|
|
O sea, un poco menos que las dos fuerzas juntas... eso te enseña que si un grupo quiere ser eficiente, tienen que tirar todos para el mismo lado.
Bueno, te dejo a vos que repitas lo mismo para el resto de los ángulos.
Vamos a la pregunta b). Si te funciona bien el hipocampo tenés que darte cuenta de que la equilibrante se encuentra en el mismo plano que las dos fuerzas, sea cual sea el ángulo entre ellas. Si así no fuese no podría equilibrarlas, ya que su componente fuera del plano ( o si querés: en el eje z) no estaría equilibrando una componente de las fuerzas. |
|
|
| |
|
|
| |
|
 |
| DESAFIO: ¿Y si α vale 0 grados? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
|

