NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
|
FIS s1.01- Hallar gráfica y analíticamente el módulo y
la dirección de la fuerza equilibrante del siguiente
sistema de fuerzas concurrentes aplicadas a un
cuerpo: F1 = 4,5 kgf hacia el noreste; F2 = 2,3 kgf hacia el este y F3 = 1,4 kgf hacia el sur. |
| Manos a la obra. Lo primero el DCL. Sobre el que vamos a hacer una resolución gráfica. Tené en cuenta que la direcció NE forma 45º con el E. |
|
|
| |
|
|
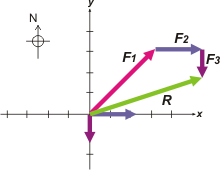
| Sumar vectores, gráficamente, se puede hacer de varias maneras. Una de ellas es dibujar cada vector a continuación del otro, no importa el orden. Yo lo voy a hacer así: en el orden 1,2,3, ¿ok?. Luego la suma es otro vector, que voy a llamar R (por resultante) cuyo origen coincide con el origen del primero, y su extremo con el extremo del último. Miralo. |
|
|
 |
|
|
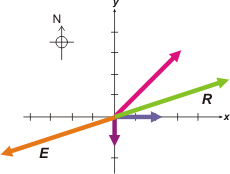
| La equilibrante, E, es la fuerza igual y contraria a la resultante. E = — R |
|
|
 |
|
|
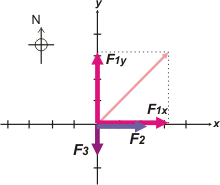
| Ahora vamos a la resolución analítica. Para eso tenemos que sumar los tres vectores, pero ya sabemos que los vectores no se suman alegremente como números, sobre todo cuando no son codireccionales. Eso es lo que pasa justamente con el vector F1. Lo que vamos a hacer es descomponer F1 en sus componentes norte y este y luego sumar todo los que apunte en la dirección x por un lado y todo lo que apunte en la dirección y por el otro. |
|
|
 |
|
|
Para hacer las sumas no olvides que
F1x = F1 . cos 45º = 3,18 kgf
F1y = F1 . sen 45º = 3,18 kgf
Entonces
Σ Fx = F1x + F2 = 3,18 kgf + 2,3 kgf = 5,48 kgf
Σ Fy = F1y — F3 = 3,18 kgf — 1,4 kgf = 1,78 kgf
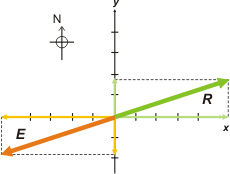
Ya trenemos las componentes de la resultante. Te las represento en el gráfico. Las de la equilibrante son justamente las contrarias, E = — 5,48 kgf i — 1,78 kgf j |
|
|
 |
|
|
| |
|
|
| DISCUSION: Como ves llegamos al mismo resultado. Ya sea por el método gráfico como el analítico. Si sumáramos F1 más F2 más F3 más E, esa sumatoria daría cero y el cuerpo estaría en equilibrio. Por otro lado, mirá lo que sale... y pensá bien en esto... Cualquier fuerza que integre la sumatoria de fuerzas de un cuerpo que está en equilibrio es la equilibrante de el resto. Qué me contás. |
|
 |
| DESAFIO: Hallar el módulo de la resultante de este problema y el ángulo que forma con la dirección x. (¡Que es lo que pedía el enunciado! ¡Jua, jua!). |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización set-06. Buenos Aires, Argentina. |
|
|
|

