 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
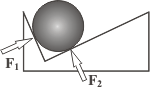
NMS s1.04*-. La bola del dibujo está en apoyada entre dos planos inclinados. Los módulos de las fuerzas de las superficies se indican como F1 y F2 y el módulo de la fuerza peso de la bola es P. Entonces: |
 |
|
a) F1 < F2 P < F1 + F2 d) F1 < F2 P = F1 + F2
b) F1 = F2 P > F1 + F2 e) F1 > F2 P > F1 + F2
c) F1 > F2 P < F1 + F2 f ) F1 > F2 P = F1 + F2
|
|
|
Este problema es sencillísimo. Pero... tal vez, tiene una o dos dificulatades. Se trata de unas pocas cuestiones demasiado obvias como para que alguien te las haya enseñado... y hasta que vos no te tropezás con esas piedras, y te hacés un lindo chichón, no aprendés a esquivarlas. |
|
|
|
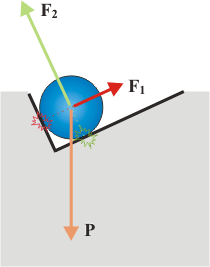
La primera de esas obviedades que te voy a indicar es que este cuerpo extenso se comporta como un cuerpo puntual. Las fuerzas que actúan sobre él son: P, su peso, F1 y F2, los contactos con las paredes inclinadas.
Las fuerzas de contacto se transmiten dentro del sólido en línea recta por lo tanto las tres fuerzas actúan sobre el centro de masa de la bola, son tres fuerzas concurrentes actuando sobre un único punto.
En su versión canónica, estándar, y ya procesada, el DCL de la bola tiene la pinta que te muestro acá al lado. La costumbre de representar las fuerzas con vectores cuyo origen se sitúa en el punto donde actúa la fuerza suele evitar muchos errores. |
|
|
|
| Tengo que confesarte que el DCL que dibujo está a escala, y por lo tanto podría responder el ejercicio correctamente sólo mirando el dibujo (la respuesta correcta es la a)). Reconozco que así no vale. Te voy a plantear un razonamiento (debe haber varios) por los que arribar a la respuesta correcta aún con una representación fuera de escala. |
|
|
|
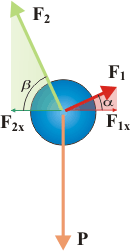
En cuanto a la comparación entre F1 y F2, lo primero que hay que tener en cuenta es que F1 es la fuerza que hace el plano más inclinado, el de la izquierda, y F2, el que hace el plano menos inclinado, el de la derecha (éste juega más de piso, el otro juega más de pared, ¿ok?)
Después de esta sugerente descripción, acordarás que el plano que esté más inclinado hará una menor fuerza, y viceversa. Pero aunque lo veas con la intuición, vamos a ver un método analítico para zanjar cualquier duda.
Las componentes horizontales de ambas fuerzas deben ser iguales (si así no fuera, en cuerpo no podría estar en equilibrio).
F1x = F2x
siendo
F1x = F1 cos α y F2x = F2 cos β
|
|
|
|
de modo que
F1 cos α = F2 cos β
cuanto mayor es un ángulo, menor es su coseno, de modo que no cabe otra posibilidad que F2 se mayor que F1. Se trata de una verdad palmaria que es más fácil verla en el dibujo que a través de la ecuación. Pero es, no cabe duda.
La segunda premisa de las resuestas habla de la suma de las fuerzas F1 y F2. Pero se preocuparon en aclararnos que se referían a los módulos de las fuerzas (tené eso presente porque es muy importante). |
|
|
|
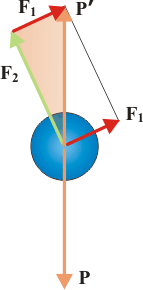
Está claro que la suma vectorial de F1 y F2 debe ser igual a la equilibrante de P, a la que llamaré P'. Dicho en una ecuación:
P' = F1 + F2 (suma vectorial)
Y acá aparece la respuesta. Sea cual fuera el tamaño relativo con que hayas dibujado F1 y F2, la suma vectorial entre dos vectores se resuelve gráficamente con un triangulito construido de esta manera: dibujando uno a continuación del otro (da lo mismo en qué orden).
En todo triángulo se verifica que cualquier lado es menor que la suma de los otros dos. En conclusión la suma de los módulos de F1 y F2 debe ser mayor que el módulo de P', y por lo tanto mayor, también, que el módulo de P.
Una sola de todas las respuestas posibles reune las dos conclusiones que sacamos hasta ahora. |
|
|
|
| |
F1 < F2 P < F1 + F2 |
respuesta a) |
|
|
|
| DESAFIO: En una parte del desarrollo de este ejercicio había concluido que el plano más inclinado hacía una fuerza menor. En una situación extrema uno de los dos planos esta horizontal y el otro vertical. El menos inclinado (el horizontal se tiene que bancar todo el peso, y el vertical, nada, cero). Ahora bien. Si ambos planos estuviesen muy inclinados, cercanos a los 90 grados... digamos 85 grados ¿los dos hacen poca fuerza? |
|
 |
| |
|
| *Este ejercicio fue parte del examen parcial del CBC tomado en mayo de 2007 en la banda horaria de martes y viernes por la mañana. |
|
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se prohibe su utilización sin resolver los desafíos. Última actualización may-07. Buenos Aires, Argentina. |
|
|

