NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |

|
NMS s1.01- Hallar la tensión en las cuerdas, si el peso
que soporta es de 200 kgf. |
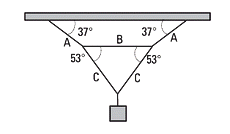 |
La pregunta inmediata cuando se encara por primera vez un ejercicio como éste es: ¿a qué cuerpo le aplico las propiedades del equilibrio? Si lo hacemos con el único que aparece en el sistema no vamos a poder plantear nada sobre las sogas que no están en contacto con él...
La solución es pensar en un cuerpo imaginario (tal vez no tanto) como un pedacito de soga, un nudo, un encuentro. No nos importa qué cantidad de soga, no nos importa su masa, ya que como está en equilibrio no interviene en el problema.
Por ejemplo el nudo en el que concurren las sobas A, B y C... (lo llamé nudo 2) está en equilibrio, le aplicamos el principio del equilibrio a él. Otro tanto podemos hacer con el nudo de abajo (lo llamé nudo 1) donde concurren las cuerdas C y la vertical que sostiene cuyo peso conocemos. Yo diría que ésa es la punta del ovillo. |
|
|
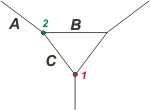 |
Podrás preguntarte por las otras cuerdas que no van a aparecer en el equilibrio de esos nudos. Se trata de un asunto de simetría: hasta les pusieron el mismo nombre porque realizan la misma fuerza, su disposición simétrica no les permite hacer otra cosa.
No conviene abusar de los criterios de simetría, pero acá es tan obvio que no hacerlo sería casi un insulto. |
|
|
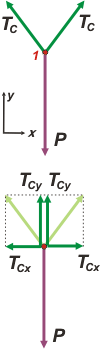 |
Bien, entonces vamos a los DCL de esos dos nudos. Sobre el nudo 1 actúan tres cuerdas, tres fuerzas que son TC, hacia arriba a la izquierda, TC hacia arriba a la derecha y una soga que tira hacia abajo que es igual al peso del cuerpo, la llamaré directamente P, ¿ok?
Las fuerzas no son colineales de modo que elegimos un SR y descomponemos las fuerzas que no coincidan con la dirección de los ejes. Mi experiencia me indica que el SR más económico es el que te dibujé (horizontal-vertcal). Supongo que vos hubieras elegido el mismo.
De este modo aparecen nuestras primeras dos ecuaciones:
eje x → TCx — TCx = 0 [1]
eje y → 2 TCy — P = 0 [2]
Si bien desaparecen los valores de las fuerzas, aparecen los de sus componentes, ya los vamos a relacionar. |
|
|
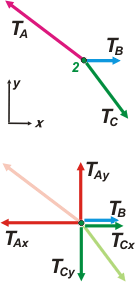 |
Ahora le llega el turno al DCL del nudo 2. Ocurre lo mismo que antes, de modo que con el mismo SR descompongo las fuerzas que quedan oblicuas y así llegamos al segundo par de ecuaciones
eje x → TB + TCx — TAx = 0 [3]
eje y → TAy —TCy = 0 [4]
TCx y TCy, que aparecen acá, ya aparecieron en las de arriba. El círculo se está cerrando. Para poder relacionar las componentes de cada fuerza con la fuerza verdadera vas a tener que prestar atención a los triángulos rectángulos que se forman cada vez que descomponés un vector.
Además tenés que rebuscártelas para encontrar ángulos que sean congruentes (un modo fino de decir iguales) |
|
|
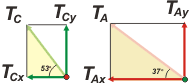
Acá te muestro los triángulos rectángulos de los que surge que:
TCx = TC . cos 53º y TCy = TC . sen 53º
TAx = TA . cos 37º y TAy = TA . sen 37º |
|
|
|
Ahora metemos todo en la licuadora algebraica y vamos sacando conclusiones. De [2] sale que TCy = 100 kgf , entonces con dividirlo por sen 53º sabremos que |
|
|
|
Si ahora a ésto lo multiplicamos por el cos 53º, aparecerá TCx = 75 kgf . De la ecuación [4] tendremos que TAy = 100 kgf , de modo que dividiéndolo por sen 37º aparecerá |
|
|
|
Casi repitiendo los mismos pasos a ése lo multiplicamos por cos 37º, aparece
TAx = 133 kgf y con este valor voy a la ecuación [3], de donde surge |
|
|
|
| |
 |
| |
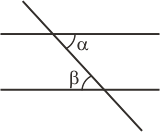
| Solo porque sos una buena persona te voy a revelar un secreto, que es el siguiente. Yo sabía que los ángulos que te indiqué en los triangulitos de descomposición vectorial eran los que te marqué y tenían el valor que te indiqué porque me acordaba de una cosa que me enseñó mi maestra de 5to. grado: los ángulos alternos internos entre paralelas son congruentes. Yo estaba enamorado de esa maestra, pero eso no se lo cuentes a nadie. |
 |
|
|
| DESAFIO: ¿Cuál es el máximo peso que se puede colgar si la soga B soporta un máximo de 100 kgf? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

