TRABAJO Y ENERGIA, Ead42, fisica online, ejercicios resueltos

home

más de trabajo y energía

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica, elásticos)

42 - El coche de un ascensor, de 400 kg, está en reposo en el primer piso, a 3 m de altura sobre el extremo libre de un resorte paragolpes cuya constante elástica es 19200 N/m. En esas condiciones se rompe el cable que lo sostiene, y automáticamente actúa un freno de fricción contra las guías que le aplica una fuerza vertical en sentido opuesto a su desplazamiento, cuyo módulo constante es 1600 N. Hallar:
a- la velocidad del coche al llegar al extremo del resorte.
b- la máxima distancia que lo comprimirá.
c- la altura máxima que alcanzará, luego del primer rebote.

¿Sabías que los ascensores tienen frenos automáticos (mordazas sobre los rieles) y resortes paragolpes en el fondo del foso? Es verdad. También es cierto que no siempre funcionan bien. Veamos qué ocurre en este caso.

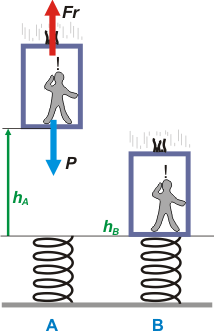Vamos a comparar los estados A y B, pero antes vamos a caracterizarlos correctamente. El instante A es cuando se cortan las cuerdas, y comienza a actuar la fuerza de frenado. El instante B es cuando el ascensor toca (pero todavía no comprime) el resorte.

Los comparamos energéticamente. Voy a elegir como cero de las alturas el nivel de la espira libre del resorte. O sea, la altura del ascensor en B será 0. El resto de las alturas lo miso desde ahí.

W_FncAB= ΔE_MAB

La única fuerza no conservativa es la del frenado, por lo tanto

W_Fr= E_MB— E_MA

Fr . h_A . cos 180º = E_CB— E_PA

En A el ascensor parte del reposo, de modo que sólo posee energía potencial. Y En B (debido a la elección del SR) sólo cinética.

Fr . h_A . cos 180º = ½ m v_B² — m g h_A

En esa expresión, la única incógnita es la velocidad en B (que es una de las preguntas del enunciado). La despejamos y calculamos.

v_B² =		— Fr . h_A + m g h_A

		½ m

v_B² =		— 1.600 N . 3 m + 400 kg . 10 m/s² . 3 m

		½ 400 kg

v_B = 6 m/s

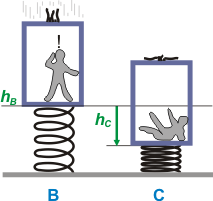
Para continuar podríamos comparar energéticamente A con C (es lo recomendable), o B con C. Voy a optar por lo segundo, pese a mis convicciones. Después analizaremos por qué digo esto.

Entonces:

W_FncBC= ΔE_MBC

Debemos suponer que los frenos siguen actuando durante el recorrido de longitud h_C (no hay nada que justifique lo contrario).

W_Fr_BC= E_MC— E_MB

Fr . h_C . cos 180º = E_PC+ E_EC — E_CB

La compresión del resorte (hasta C) no es otra cosa que la altura del ascensor (medida desde la espira libre, o sea h_C).

— Fr . h_C = — m g h_C+ ½ k h_C² — ½ m v_B²

De este modo nos queda una única incógnita que no es otra que la que solicita el enunciado. La ecuación es cuadrática. Tenés que reordenar, agrupar, y finalmente usar la fórmula salvadora de los griegos. Te dejo a vos la última parte, ¿dale?

½ k h_C² + (Fr — m g) h_C— ½ m v_B² = 0

9.600 N/m h_C² + 2.400 N h_C— 7.200 J = 0

4 N/m h_C² + 1 N h_C— 3 J = 0

h_C = — 1 m

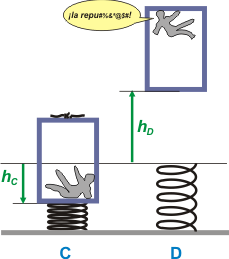
Tuve que descartar un resultado posible, ¿cómo lo habré hecho? Bueno, sigamos. Veamos hasta dónde rebota el ascensor. Para eso voy a comparar los instantes C con D, aunque también podría hacerlo comparando B con D o inclusive (y es el más indicado de todos) A con D.

Entonces:

W_FncCD= ΔE_MCD

Debemos suponer que los frenos siguen actuando durante el recorrido hacia arriba (no hay nada que justifique lo contrario).

W_Fr_DC = E_MD— E_MC

El trabajo que hace la fuerza de frenado (la única no-conservativa que actúa) lo realiza durante todo el trayecto de subida, que en números absolutos, vale h_C + h_D.

Y además sigue siendo un trabajo negativo, porque durante la subida la fuerza de frenado apunta hacia abajo.

En C tenemos energía potencial gravitatoria y elástica. En D sólo potencial gravitatoria.

Fr . (h_D — h_C) . cos 180º = E_PD — E_PC— E_EC

— Fr . (h_D — h_C) = m g h_D — m g h_C — ½ k h_C²

Nuevamente una única incógnita, h_D. Reordenamos, agrupamos y despejamos:

— Fr h_D — m g h_D = — m g h_C — ½ k h_C² — Fr . h_C

Fr h_D + m g h_D = m g h_C + ½ k h_C² + Fr . h_C

h_D =		m g h_C + ½ k h_C² + Fr . h_C

		Fr + m g

h_D =		400 kg 10 m/s² (-1 m) + 9.600 N/m (-1 m)²* + 1.600 N . (-1 m)*

		1.600 N + 400 kg 10 m/s²

h_D =		— 4.000 Nm *+ 9.600 Nm* — 1.600 Nm

		5.600 N

h_D = 0,714 m

En esa cuenta es fácil caer en errores de signos provenientes del valor negativo de h_C. Siempre es preferible (cuando se puede) elegir comparar dos instantes en los que sólo se utilicen datos aportados por el enunciado. Si utilizás datos hallados en pasos intermedios, y contienen error, los posteriores también lo tendrán. Ese es el asunto.

DESAFIO: Hallar los ítems b) y c) utilizando solamente los datos del enunciado, es decir, comparando siempre con el instante A. Explicar qué le pasa al pasajero que metí dentro del ascensor.