NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo y energía cinética)
|
|

|
 |
Adicional 34- Un carrito de 8 kg se desliza partiendo del
reposo por un riel horizontal, con rozamiento
despreciable, cuando se le aplica una fuerza resultante
cuya componente horizontal varía como
lo muestra el gráfico adjunto, donde la posición
x = 0 corresponde al estado de partida.
|
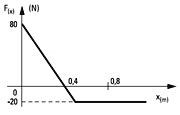 |
| Determinar qué velocidad tendrá el móvil en
las posiciones x1 = 0,4 m, y x2 = 0,8 m. Determinar
en qué posición se detendrá nuevamente (si
se detiene). |
|
Que no cunda el pánico: se trata de otro sencillo ejercicio de trabajo, calculado mediante el método geométrico de integración de áreas (cálculo de áreas).
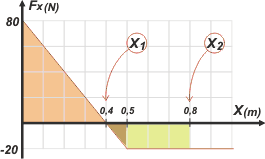
Rehice el gráfico porque adolece de un defecto importante: no está suficientemente claro qué fuerza se corresponde con la posición x1 = 0,4 m. En el mío sí. Yo saqué el valor correcto y te planteo que vos también lo hagas en el desafío. |
|
|
 |
Entonces tenemos que el trabajo de la resultante es igual a la variación de energía cinética:
WRes = ΔEc
Y eso es igual, también, al trabajo de la componente de la resultante en la dirección del desplazamiento (ya que la componente normal no realiza trabajo).
W0-1 = ΔEc0-1
|
|
|
|
Ese trabajo lo calculamos como el área encerrada bajo la curva en el intervalo 0-1. Se trata de un simple triangulito (base por altura sobre dos) de modo que:
W0-1 = Area0-1 = ½ 80 N . 0,4 m = 16 J
16 J = Ec1 — EcO
Como parte del reposo, la energía cinética inicial vale cero.
16 J = Ec1
16 J = ½ . m . v1²
16 J = ½ . 8 kg . v1²
|
|
|
|
|
|
Para obtener la velocidad en la posición x2 = 0,8 m se procede de la misma manera. El único cuidado que hay que tener es que las áreas emplazadas debajo del eje de las posiciones tienen signo negativo. Las nuevas áreas que tenés que calcular te las coloreé en marrón y verde. A ver si llegamos a lo mismo:
W0-2 = Area0-2 = 16 J — 1 J — 6 J = 9 J
9 J = Ec2
9 J = ½ . m . v2²
9 J = ½ . 8 kg . v2²
|
|
|
|
|
|
| Si el movimiento continúa con fuerza constante, en ese caso, sí ha de detenerse. Para hallar esa posición simplemente habrá que hallar un área bajo la curva igual al área sobre la curva (de 16 J). Es fácil, el triángulo amarillo ya representa un joule negativo... nos faltan 15. Cada cuadradito verde representa dos joules... entonces necesitamos 7,5 cuadraditos. (¿Me seguiste?). Bueno... tratá de hacer un planteo formal y correcto. Pero la respuesta -si llamamos xF a la posición en la que se detiene el móvil- es: |
|
|
|
|
|
ESAFIO: ¿En qué posición la velocidad es la máxima de todo el recorrido? |
|
 |
| Algunos derechos reservados.
Se prohibe terminantemente imprimir en blanco y negro. Severísimas penas a los transgresores de esta prohibición. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
|

