 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Leyes de conservación, trabajo) |
|
|

|
| |
 |
Adicional 30) Determinar el trabajo que realiza la fuerza
que ejerce un señor sobre su portafolios, de
4 kg, en los siguientes casos, que son algunas de
las etapas de su viaje:
a- Lo sostiene durante media hora, mientras
espera al colectivo.
b- Corre con él 4 m, con velocidad constante
horizontal, para alcanzarlo.
c- Lo levanta 1,2 m al entrar al mismo.
d- Lo baja en la terminal, caminando por una
rampa de 20 m de longitud, que forma un ángulo
de 10° con la horizontal.
|
|
|
En todas las preguntas de este ejercicio se trata de fuerzas constantes hechas por el pobre profesor sobre su portafolios. Como son fuerzas constantes, el trabajo puede calcularse con la expresión:
WF = F . Δx . cos α
Vamos con el primero:
a- Lo sostiene durante media hora, mientras
espera al colectivo. |
|
|
 |
Como el tío está parado, ni él ni su portafolios se mueve, luego:
Δx = 0
Wa) = 40 N . 0 m . 1 |
|
|
|
|
|
|
| b- Corre con él 4 m, con velocidad constante
horizontal, para alcanzarlo. |
|
|
 |
Ahora hay desplazamiento, pero -a menos que haga bailar al portafolios- mantiene la fuerza de su brazo perpendicular al desplazamiento, entonces:
cos 90º = 0
Wb) = 40 N . 4 m . 0 |
|
|
|
|
|
|
| c- Lo levanta 1,2 m al entrar al mismo. |
|
|
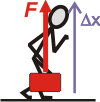 |
En este caso el desplazamiento vale 1,2 m y el ángulo entre el desplazamiento y la fuerza 0º.
Wc) = 40 N . 1,2 m . 1 |
|
|
|
|
|
|
| d- Lo baja en la terminal, caminando por una
rampa de 20 m de longitud, que forma un ángulo
de 10° con la horizontal. |
|
|
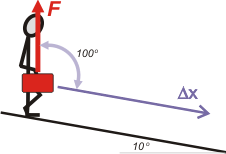 |
Bueno... no hay secretos:
cos 100º = — 0,174
Wd) = 40 N . 20 m . (— 0,174) |
|
|
|
|
|
|
| e) Lo levanta 0,5 m con aceleración constante de 1 m/s² |
|
|
 |
Lo que cambia ahora es la fuerza que hace el profe. Te dejo el cálculo a vos. Bueno... no hay secretos:
cos 0º = 1
Wd) = 44 N . 0,5 m . 1 |
|
|
|
|
|
|
Discusión: Como ves, trabajo en Física, no significa lo mismo que trabajo en el mercado laboral... |
|
 |
| |
|
| DESAFIO: ¿De dónde salieron los 44 N del último ítem? |
|
| Algunos derechos reservados.
Severísimas penas a quien se arrojase desde un avión en vuelo sin paracaídas. Se permite su reproducción citando la fuente. Última actualización may-13. Buenos Aires, Argentina. |
|
|
|

