NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Trabajo y energía)
|
|

|
Adicional NMS 20* - Un hombre empuja horizontalmente una caja de 30,0 kg una distancia de 4,50 m sobre un piso horizontal con velocidad constante. El coeficiente de rozamiento cinético entre el piso y la caja es de 0,25.
a) ¿Qué magnitud de fuerza debe aplicar el hombre?
b) ¿Cuánto trabajo realiza sobre la caja?
c) ¿Cuánto trabajo efectúa la fuerza de fricción sobre la caja?
d) ¿Cuánto trabajo realiza la fuerza de apoyo?
e) ¿Cuánto trabajo realiza el peso?
f) ¿qué trabajo total se efectúa sobre la caja? |
|
Este ejercicio es muy sencillo, y lo desarrollo fundamentalmente para mostrarte una de las propiedades más interesantes del trabajo.
|
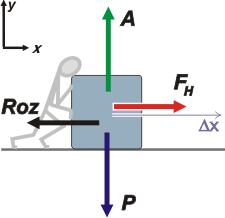 |
Según la descripción que hace el enunciado, sobre la caja están actuando cuatro fuerzas: la fuerza que realiza el hombre, FH; la fuerza de fricción, Roz; la fuerza de apoyo, A; la fuerza peso, P.
La primera pregunta es una cuestión pura de dinámica. Para que la caja se mueva a velocidad constante el hombre debe realizar una fuerza igual y contraria a la fuerza de rozamiento. |
|
|
|
Para no equivocarnos hacemos un DCL, elegimos un SR y planteamos las ecuaciones de Newton.
FH — Roz = 0
A — P = 0
Por suerte conocemos la naturaleza de las fuerzas de rozamiento y sabemos que es igual al producto entre el coeficiente de rozamiento dinámica y la fuerza que comprime las superficies en rozamiento:
Roz = μd . A
Roz = 0,25 . 300 N
Roz = 75 N
De donde: |
|
|
|
|
|
Las preguntas siguientes son sencillos cálculos de trabajo. Empecemos con el trabajo de la fuerza que hace el hombre.
WFH = FH . Δx . cos αF
donde αF es el ángulo que forman la fuerza que hace el hombre con el desplazamiento, que vale 0º
WFH = 75 N . 4,5 m . 1
|
|
este planteo del trabajo podemos realizarlo ya que la fuerza es constante |
|
|
|
El trabajo que realiza la fuerza de rozamiento valdrá:
WRoz = Roz . Δx . cos αR
donde αR es el ángulo que forman la fuerza de rozamiento con el desplazamiento, que vale 180º
WRoz = 75 N . 4,5 m . (-1)
|
|
|
|
|
|
El trabajo que realiza la fuerza peso valdrá:
WP = P . Δx . cos αP
donde αP es el ángulo que forman la fuerza peso con el desplazamiento, que vale 90º
WP = 300 N . 4,5 m . 0
|
|
|
|
|
|
Por último, el trabajo que realiza la fuerza de apoyo valdrá:
WA = P . Δx . cos αP
donde αA es el ángulo que forman la fuerza de apoyo con el desplazamiento, que vale 90º
WA = 300 N . 4,5 m . 0
|
|
|
|
|
|
La propiedad que quería mostrarte es la siguiente: la suma de todos los trabajos de todas las fuerzas que actúan sobre un cuerpo es igual al trabajo de la resultante WRes, que no es otra cosa que el trabajo total que pregunta el enunciado.
WRes = WFH + WRoz + WP + WA
WRes = 337,5 J + (— 337,5 J) + 0 J + 0 J
|
|
|
|
|
|
Lo que por otro lado no debe sorprendernos, ya que el trabajo de la resultante es igual a la variación de energía cinética que en este caso ya sabíamos que valía cero porque la caja se desplaza a velocidad constante, o sea, sin variar su velocidad.
|
|
 |
| *Este ejercicio pertenece a la guía de problemas de la asignatura Física Mecánica de la Universidad Tecnológica de Chile. |
|
|
| DESAFIO: ¿A qué velocidad se desplaza la caja? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-12. Buenos Aires, Argentina. |
|
|
|

