 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica) |
|
|

|
| |
| Adicional No me salen 14) Un péndulo ideal, cuya partícula tiene masa m siendo la longitud del hilo desconocida, inicialmente parte del reposo con Θ medido desde la posición de equilibrio. El soporte S en el techo, se diseñó para aguantar una fuerza máxima de 1,5 veces el peso de m. ¿Se podrá usar el péndulo para cualquier valor de Θ sin que se rompa S? |
|
|
Nota: Enviado por mi amigo Nicolás Lacovich especialmente para No me salen.
Se trata de un péndulo simple de masa m, que cuelga de un hilo que supondremos ideal. Esta aclaración es importante porque los piolines ideales (sin masa, inextensibles e importados) realizan la misma fuerza en ambos extremos; de modo que si el amarre en el techo soporta una fuerza máxima de 1,5 veces el peso de la masa entonces, en esa situación límite, también realiza sobre la masa una fuerza de 1,5 veces su peso.
Además tenemos el problema de que la longitud del hilo -que llamaré R, por ser igual al radio de giro- es desconocida. Qué problema... apostaría guita a que no es necesario conocer su valor. |
|
|
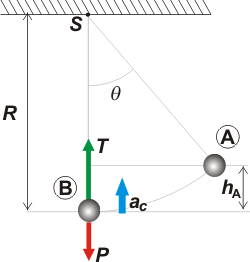 |
La masa se suelta desde la posición A, y desciende por una trayectoria circular pasando por la posición B en la que el hilo ejerce la máxima tensión de todo el recorrido (después voy a abundar en ese concepto).
Por lo tanto la situación de peligro de ruptura se halla justamente en B. Hagamos el DCL de la masa en ese instante y apliquemos la Ley de Newton. Las únicas fuerzas que actúan sobre el cuerpo son su propio peso, P y la tensión de hilo T (que si es la máxima permitida, vale 1,5 P).
No te olvides que P = mg. |
|
|
|
T — P = m ac
La aceleración es de tipo centrípeta, porque la masa está girando sobre una circunferencia de radio R. Entonces...
1,5 P — P = m vB²/ R
0,5 m g = m vB²/ R
0,5 g = vB²/ R
De esa expresión podemos despejar vB², que es el cuadrado de la velocidad máxima permitida sin ruptura del soporte.
vB² = 0,5 R g
Por otro lado, podemos igualar las energías mecánicas de las posiciones A y B. Ya que no hay fuerzas no-conservativas actuando. Tomemos el cero de las alturas en la posición más baja (considerando que el cuerpo es puntual).
EMA = EMB
m g hA = ½ m vB²
g hA = ½ vB²
Reemplacemos vB² por su equivalente que sacamos antes:
g hA = ½ 0,5 R g
hA = 0,25 R
La altura de A se puede expresar en función del ángulo Θ y del radio de giro. Si no te das idea de cómo hacerlo, prestale atención al triangulito formado con vértice en S.
R (1 — cos Θ) = 0,25 R
Lo sabía: el largo del hilo se cancela, no importaba cuánto valía.
(1 — cos Θ) = 0,25
cos Θ = 0,75
|
|
|
| |
Θ = 41,4° |
el máximo ángulo sin riesgo |
|
|
|
Prometí explicar por qué siempre la fuerza es mayor en el punto más bajo... tal vez ya te hayas dado cuenta. Es obvio que cuanto más bajo está el péndulo mayor es su velocidad (todos lo recordamos de cuando jugábamos en la hamaca)... es algo que la conservación de energía asegura. Si la velocidad es mayor, entonces, la aceleración centrípeta también será mayor... por lo tanto la fuerza que tira hacia el centro (en nuestro caso T) también ha de ser mayor.
DESAFIO: ¿Cuánto debe resistir el soporte si se suelta la masa desde un ángulo de 60° con la vertical? |
|
 |
| |
| |
|
| Algunos derechos reservados.
Severísimas penas a quien orinase en un paso a nivel sobre la vía electrificada. Se permite su reproducción citando la fuente. Última actualización feb-11. Buenos Aires, Argentina. |
|
|
|

