 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
Adicional No me salen E8 - Sobre un resorte ideal descargado se realiza un trabajo L para estirarlo un valor ΔX. Si a partir de esta posición, se lo quiere estirar ½ ΔX más. El trabajo que se deberá realizar será:
1) L 2) (3/4) L 3) 2L 4) 3L 5) (3/2) L 6) (5/4) L
|
| Como ves en las opciones la respuesta habrá que darla en función de L, el trabajo que costó el primer estiramiento. Para ir calentando los motores te muestro un gráfico de la fuerza que debió realizarse para ese primer estiramiento. |
|
|
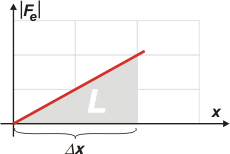 |
Vamos a suponer que la fuerza que trabaja es siempre igual a la elástica (estira el resorte suavemente prácticamente sin aceleración). Entonces esa fuerza debe tener una gráfica como la que te hice, ya que la fuerza elástica vale siempre:
|Fe| = k . ΔX
Y como en todo gráfico de fuerza en función del desplazamiento, el área encerrada bajo la curva representa el trabajo de esa fuerza. |
|
|
|
De modo que si quisiéramos darle una expresión algebraica al trabajo en este primer estiramiento debemos hacer un cálculo de área (que es este caso es muy sencillito ya que se trata de un triángulo)...
L = ½ k . ΔX²
Tené ese resultado presente, porque lo vamos a usar en breve. |
|
|
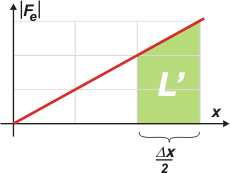 |
El trabajo necesario para estirarlo un poco más (precisamente la mitad del primer estiramiento), que voy a llamar L', tenemos que representarlo en el mismo gráfico para poder comparar.
Es obvio que la fuerza que hay que realizar es mayor que la anterior... porque, claro, el resorte ya arranca estirado.
Para calcular ese trabajo podemos hallar el área correspondiente. |
|
|
|
Y después comparamos las áreas y damos la respuesta en función de el primer trabajo, L. |
|
|
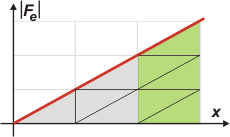 |
Pero ya que me tomé el trabajo de hacer unos gráficos tan prolijos, animémonos a compararlos gráficamente.
Para eso tracé unas rayitas que dividen las áreas en porciones todas iguales (triangulitos pequeños) que si los contás, hay 4 en el trabajo inicial, L, y 5 en el siguiente, L'. |
|
|
|
Luego, el trabajo posterior es 5/4 veces el trabajo inicial... y ya encontramos la respuesta correcta al ejercicio.
Pero claro... vos me vas a decir que eso fue fácil porque yo usé el ingenio... y así no vale... no es el estilo No me Salen... y tenés razón. No sólo por eso, sino porque el método funcionó aquí, donde las relaciones entre los desplazamientos son fracciones enteras... si así no fuese... quién podrá salvarnos... Lo correcto es saber resolverlo analíticamente.
El área verde, L', se puede obtener como diferencia entre el área total, (L + L'), y el área gris, o sea L. Las tres áreas son triángulos:
L' = (L + L') — L
La base del triángulo grande vale (3/2) ΔX, y su altura k (3/2) ΔX...
L' = (½ k . [(3/2) ΔX]² ) — ½ k . ΔX²
L' = (½ k . (9/4) ΔX² ) — ½ k . ΔX²
L' = ½ k . ΔX² [(9/4) — 1]
L' = ½ k . ΔX² (5/4)
|
|
|
| |
L' = (5/4) L |
respuesta 6) |
|
|
|
DISCUSION: Espero que me hayas podido seguir todos los pasos algebraicos, que son muy sencillos.
|
|
 |
| DESAFIO: ¿Cuánto podría estirarse el resorte realizando un trabajo total de 2,25 L? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se permite su impresión pero en escala de grises es una cagada. Está totalmente prohibido ingresar a la playa con el torso desnudo. Última actualización mar-09. Buenos Aires, Argentina. |
|
|
|

