NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica, choque explosivo)
|
|

|
Adicional No me salen E5* - Sobre una superficie horizontal sin rozamiento, un resorte de constante elástica k = 0,3 N/m está comprimido 10 cm entre dos masas de 0,5 kg y de 1 kg. Si dejamos de comprimir el resorte:
a) ¿Cuál es la energía cinética de los dos cuerpos después de separarse del resorte?
b) ¿Cuál es la energía cinética de cada cuerpo?
|
* Este ejercicio se tomó en un 2do. examen parcial en Ciudad Universitaria en julio de 2007. Es muy interesante en varios aspectos. por un lado aparecen las simetrías temporales (el antes y el después) que acreditan eso de "choque explosivo" y por otro lado las leyes de conservación de energía y de cantidad de movimiento.
Siempre un esquema aclara y ordena los tantos. Aprendé a hacerlos, es una pavada. No están acá sólo para que vos entiendas de qué te hablo. Están, también, para que aprendas a comunicar la física, comunicar la ciencia. |
|
|
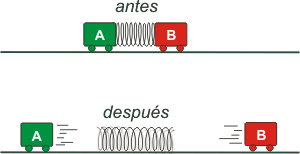 |
Cuando el resorte se suelta empuja a ambos cuerpos por igual, con la misma fuerza y durante el mismo tiempo. El proceso es demasiado complicado como para hacer descripciones físicas de las cuales extraer resultados. Es mucho más fácil comparar energéticamente el antes con el después. |
|
|
|
La variación de energía mecánica entre el antes y el después debe ser igual al trabajo de las fuerzas no-conservativas que hayan actuado durante el proceso. En nuestro caso: no hubo ninguna.
ΔEMad = WFnc
EMd — EMa = 0
EMd = EMa
La energía mecánica antes de destrabar el resorte es puramente elástica (los cuerpos están quietos). Y la energía mecánica después de liberado el resorte (cuando ya no toca a los cuerpos) es puramente cinética, y es por que que pregunta el item a) del ejercicio. La voy a llamar energía cinética total, ECT , para distinguirla de las energías sobre las que se pregunta después.
EMd = ½ k Δx²
ECT = ½ k Δx²
ECT = ½ 0,3 N/m (0,1 m)²
|
|
|
| |
ECT = 0,0015 J |
(ojos de sorpresa: ¿tan fácil era?) |
|
|
|
La segunda pregunta nos va a dar un poco más de trabajo, pero valdrá la pena. El tema es el siguiente: esa energía cinética total que acabamos de averiguar es la suma de las energías cinéticas de cada cuerpo. ¿Cuánto vale la de cada uno? Por un lado sabemos que...
ECT = ECA + ECB
supongamos que el cuerpo A es el de 1 kg y B el de 0,5 kg. Como los números me traen cierta alergia me voy a conformar con la idea de que mA = 2 mB.
Por otro lado que en toda explosión (como en cualquier choque) se conserva la cantidad de movimiento total antes y después de la explosión.
pTa = pTd
La cantidad de movimiento antes de soltarse el resorte era cero (todo estaba quieto). Y la cantidad de movimiento después se reparte en los cuerpos en forma equitativa, para que su suma sea cero.
pTdA = pTdB
mA vA = mB vB
o lo que es lo mismo
2 mB vA = mB vB
de donde concluimos que
2 vA = vB
con esta información interesante vuelvo a la ecuación de energía. A ver...
ECT = ½ mA vA² + ½ mB vB²
ECT = ½ mA vA² + ½ (½ mA) (2 vA)² = 3 ECA
|
|
|
| |
ECA = 0,0005 J ; ECB = 0,0010 J |
(llegamos) |
|
|
|
El cuerpo más liviano sale despedido más velozmente. Como en la energía cinética cuenta más la velocidad que la masa (la velocidad aparece elevada al cuadrado) el reparto de energía termina favoreciendo al cuerpo más liviano. ¡Y no importaba cuánto valían las masas, sino la relación entre ellas! |
|
|
| DESAFIO: Sin hacer cuentas y en 30 segundos: ¿cuánto valdrá la energía total si el resorte tuviese una constante el doble que la del problema? En 60 segundos: ¿cuánto si el resorte se hubiese comprimido el doble que en el problema? En 23 segundos: ¿cuánto más energía que el otro tendría un cuerpo si el primero fuese 23 veces más masivo? |
|
 |
| Algunos derechos reservados.
Se prohibe terminantemente imprimir en blanco y negro y sin citar al autor que sigue tomando mate. Última actualización jun-07. Buenos Aires, Argentina. |
|
|
|

