NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica, movimiento circular)
|
|

|
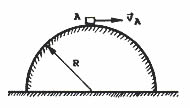
| Adicional No me salen E1* - Un cubito de hielo se desliza con rozamiento despreciable apoyado sobre un casquete esférico de radio r. Si la velocidad en el punto más alto es vA, hallar la altura a la cual se separará de la superficie, y la forma de la trayectoria que seguirá. Analizar el caso en que vA → 0 |
 |
|
Siempre dije que este era el problema más difícil de la guía, tal vez por eso lo hayan quitado. Pero no deja de ser un ejercicio excelente para trabajar en el curso. Seguramente no es para un examen, porque lleva mucho tiempo y porque tiene muchas piezas encadenadas, de modo que es fácil trabarse. Pero su capacidad de integración de diversos temas de la mecánica es profundamente aleccionadora.
Dediquémosle un párrafo a interpretarlo: parece ser que el cubito desliza sobre la superficie y en lugar de llegar al piso deslizando sobre el casquete se desprende de él a cierta altura que nos piden hallar. Parece lógico, ya que a medida que baja va ganando velocidad lateral y eso hace que, en un momento, el casquete no pueda retenerlo más a su lado. A partir de ese punto en que se separan el cubito sigue cayendo como cualquier otro cuerpo libre, en una trayectoria parabólica de tiro oblicuo.
Como todo problema de energía mecánica lo importante es que elijamos dos eventos para comparar. Parece obvio: uno de ellos será el más alto, que llamaremos A y el otro será aquel que todavía no sabemos dónde se encuentra pero que ya le ponemos nombre, se llamará S (por separación). |
|
|
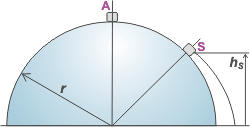 |
La comparación energética de esas dos situaciones me va a obligar a hablar de la energía potencial del cubito en S, y de ahí va a salir la altura buscada, hS.
Para el sistema de alturas, claro está, elegí ubicar el cero en la base del casquete... de modo que hA = r |
|
|
|
| Las fuerzas que actúan son conservativas, de modo que la energía mecánica en A es idéntica a la energía mecánica en S. Por si te quedan dudas sobre cuáles son las fuerzas obrantes sobre el cubito, hacemos un DCL. A falta de uno yo te hice tres |
|
|
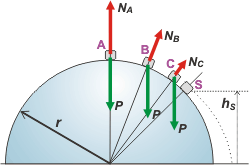 |
Los hice en las posiciones intermedias A, B, y C, cualesquiera, simplemente para mostrarte que el peso P, es siempre vertical y constante. En cambio, el apoyo sobre el casquete, N, es siempre normal a la superficie y no es constante, sino que va disminuyendo a medida que el cubito avanza.
Entonces planteamos la conservación de energía... |
|
|
|
ECA + EPA = ECS + EPS
½ m vA² + m g hA = ½ m vS² + m g hS
Como ves, ahí aparece nuestra incógnita, hS. Además, la masa del cubito multiplica en todos lados, o sea que no afecta al resultado. Y también reemplazo hA por r , que es nuestro dato.
½ vA² + g r = ½ vS² + g hS
¡Pero inesperadamente aparece una incógnita más, vS, la velocidad con que el cubito se separa del casquete...! O nos suicidamos... o le pedimos ayuda a la dinámica. Hagamos urgentemente un DCL para la situación S. |
|
|
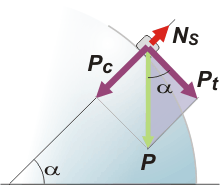 |
Como el cubito se mueve en trayectoria circular descompuse la fuerza peso en sus direcciones tangencial y radial (centrípeta). La velocidad en ese punto, vS, es tangencial a la trayectoria (como toda velocidad real, siempre) y aparece en la expresión de la aceleración centrípeta:
aCS = vS²/r
Las componentes tangencial y centrípeta del peso vamos a tener que expresarlas en función del ángulo α que forman con la vertical. |
|
|
|
Pc = P sen α
Pt = P cos α
La componente tangencial no aporta información necesaria. Nos dice que el cubito baja cada vez más rápido, pero eso ya lo sabíamos y no nos interesa. También nos dice que baja con una aceleración creciente cosa que nos preocupa un poco porque ese tipo de movimientos nunca los estudiamos... pero volvemos a tranquilizarnos, porque recordamos que la dinámica nos brinda "instantáneas" del universo, y eso es todo lo que queremos, la descripción del instante S, nada más.
Respecto a la dirección centrípeta, que es la que nos interesa, la 2da. Ley de la dinámica afirma que la suma de todas las fuerzas que actúen en esa dirección será igual al producto entre la masa del cubito y la aceleración centrípeta en ese lugar, que se puede expresar en función de la velocidad en ese lugar.
Pc — NS = m aCS
Pc — NS = m vS²/r
Sonamos. Salimos de una y nos metemos en otra peor. Apareció una nueva incógnita, ¡NS! ¿Cómo hacemos? Mirá, de acá sólo te saca el estar atento... porque situaciones como ésta acechan en todo el curso de física... se trata de una SITUACION LIMITE. ¿Te acordás qué era el punto S? Era el lugar en el que el casquete se separaba del cubito... ¿cuánto puede entonces valer la fuerza de contacto en ese lugar en el que se separan, en el que desaparece el contacto? ¡CERO! ¡NS = 0! Entiendo que si no te lo dicen, no sea inmediato verlo. Pero es bueno saber, que situaciones como ésta te están esperando detrás de cada árbol del bosque del conocimiento. Entonces queda...
P sen α = m vS²/ r
m g sen α = m vS²/ r
g sen α = vS²/ r
Y otra vez más sonamos... aparece α, ¡parió la abuela! Pero se me ocurre algo... |
|
|
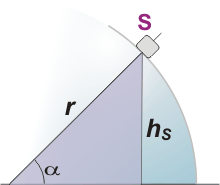 |
Mirá ese triángulo que te sombreé en (qué color es ése...) Relaciona α, con r y con hS. Hagamos desaparecer a α.
sen α = hS / r
entonces nuestra última ecuación queda así
g hS = vS²
Ahora la cosa se pone fácil. Vuelvo a la ecuación de conservación de energía... |
|
|
|
½ vA² + g r = ½ vS² + g hS
½ vA² + g r = ½ g hS + g hS
½ vA² + g r = 3 g hS / 2
Y por fin... puedo despejar nuestra incógnita |
|
|
| |
hS = ( 2 r / 3) + (vA²/ 3 g) |
|
|
|
|
| |
|
|
DISCUSION: El resultado tiene toda la descripción del problema: las unidades son correctas. Si la velocidad en A vale cero el cubito se despega a una altura igual a 2/3 del radio.
Respecto al ejercicio en sí mismo, te reitero que me parece importante. Reúne varias de las dificultades más comunes de cualquier curso inicial de Física. Cinemática, dinámica del circular, conservación de energía, geometría y trigonometría, y una situación límite muy interesante. En el punto S hay un cambio de movimiento: venía siendo circular acelerado y pasa a ser tiro oblicuo. Un instante antes de llegar a S (si se me permite semejante barbaridad) el móvil sigue teniendo todas las características propias del movimiento que traía. No es fácil abordar mentalmente los límites... pero ya te vas a acostumbrar. |
|
 |
| DESAFIO: ¿Cuál debe ser la velocidad en A, para que el cubito no deslice ni un milímetro sobre el casquete? |
|
| * Este ejercicio pertenece al libro Física del CBC que se editó hasta el año 2002, y que se utilizaba para este mismo curso. |
|
| |
|
| Algunos derechos reservados.
El uso de este material está desaconsejado por la Asociación Internacional de profesores de Física Constructivista. Se recomienda su uso clandestino en el baño de los aviones. Se permite su reproducción citando la fuente. Última actualización ene-07. Buenos Aires, Argentina. |
|
|
|

