NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, choque elástico, energía mecánica)
|
|

|
3.21- Dos esferas de masa mA y mB están suspendidas
de modo tal que en su posición de
equilibrio sus centros de masa quedan a la misma
altura. Se separa la esfera A de la posición
inicial y se la deja caer desde una altura h contra
la esfera B, con la que choca en forma perfectamente
elástica.
La relación entre sus masas es mA/mB = 3. Luego
la altura a la que llegará la esfera B será:
a) 2 h b) 1/4 h
c) h
d) 9/4 h
e) 2,5 h f) 3/2 h
|
Bueno, acá tenés un problema largo y complicado. Pero tu consigna tiene que ser: yo voy a hacer toda la física que pueda con este choque elástico. Y te aseguro, con eso alcanza.
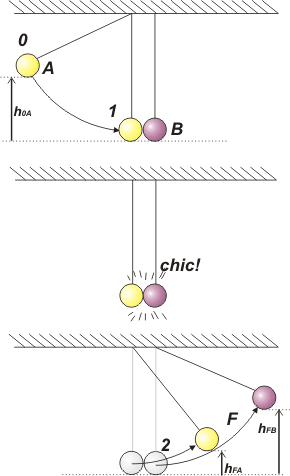
Hice una serie de esquemas con la secuencia de eventos encadenados que vincularemos de a dos, siempre de a dos. Como de costumbre, aprovecho los esquemas para ponerle nombre a los eventos y a cualquier otra variable que, después, aparezca en el desarrollo del problema. |
|
|
Bueno, acá tenés, todo empieza en el instante 0. La bola A se separa hasta alcanzar una altura h0A. Cae en un proceso estilo péndulo y en forma que, damos por supuesto, es conservativa.
Ahí choca con la bola B. La velocidad de la bola B justo antes del choque es 0, y la de la bola A no la conozco, pero se llama v1A.
El choque se produce en forma totalmente elástica. Eso nos da dos informaciones importantes: no sólo se conserva la cantidad de movimiento (del conjunto de las dos bolas) sino que también se conserva la energía mecánica del sistema bibolar (¿?).
Un instante después del choque, evento al que llamé 2, las bolas salen despedidas (en este caso ambas hacia la derecha) con distintas velocidades.
Cada una, entonces alcanzará finalmente, F, diferentes alturas. La que alcanza la bola A la llamé hFA, y la que alcanza la B, hFB. Esta última es la que pide averiguar el enunciado. Vamos a hallar ambas, que es mucho más interesante. |
 |
|
|
|
Arranquemos con la bajada de la bola A. Es una transformación conservativa de modo que
EMAo = EMA1
Si tomo el cero de alturas en la posición más baja y recuerdo que la bola A se suelta desde el reposo ("se la deja caer")...
mA g h0A = ½ mA v1A²
de donde |
|
|
|
|
|
Ahora le sigue el choque. Aunque te enojes voy a plantear las ecuaciones completas, y después tiro todo lo que sobra. Acá va la de conservación de la cantidad de movimiento, vale para TODOS los choques, sean del tipo que sean.
mA v1A + mB v1B = mA v2A + mB v2B
Y aquí la de conservación de la energía que solo se aplica en los choques perfectamente elásticos (idealmente elásticos)
½ mA v1A² + ½ mB v1B² = ½ mA v2A² + ½ mB v2B²
Ok... ahora tiramos todo lo que sobra, v1B es cero, se lleva todo el término; ½ se cancela porque aparece en todos los términos... ¡Y lo más importante! vamos a realizar un inteligente reemplazo en ambas ecuaciones, utilizando ese dato curioso que nos brinda el enunciado, a saber, que mA = 3 mB |
|
|
| |
3 mB v1A = 3 mB v2A + mB v2B |
[2] |
| |
3 mB v1A2 = 3 mB v2A² + mB v2B² |
[3] |
|
|
|
Ahora puedo cancelar las masas ya que aparecen en todos los términos. |
|
|
| |
3 v1A = 3 v2A + v2B |
[4] |
| |
3 v1A2 = 3 v2A² + v2B² |
[5] |
|
|
|
Esto ya tiene otro color. La velocidad v1A no me preocupa, ya me dice cuánto vale la ecuación [1], pero las otras dos... voy a tratar de expresar una en función de la otra. Hay miles de caminos posibles, a ver si te gusta éste. La ecuación [4] la elevo al cuadrado (ojo, mirá que el segundo miembro es un binomio), esa es la [6]. Y a ella le resto la [5] multiplicada por 3, que es la ecuación [7]. No te pierdas. |
|
|
| |
9 v1A2 = 9 v2A² + v2B2 + 6 v2A . v2B |
[6] |
| |
9 v1A2 = 9 v2A² + 3 v2B² |
[7] |
|
|
|
| Supongo que ya te diste cuenta para qué multipliqué la [5] por 3. Mirá cómo queda esa resta... [6] — [7] = [8] (viste que plomo que es el álgebra... no entiendo cómo hay gente que le gusta) |
|
|
| |
0 = 0 — 2 v2B2 + 6 v2A . v2B |
[8] |
| entonces |
|
| |
2 v2B2 = 6 v2A . v2B |
|
| y finalmente |
|
| |
v2B = 3 v2A |
[9] |
| ahora con esta sencilla relación puedo volver para atrás, por ejemplo a la ecuación [4] y reemplazarla |
| |
3 v1A = 3 v2A + 3 v2A |
|
| |
v2A = (1/2) v1A |
[10] |
| y si meto la [9] en la [10] |
| |
v2B = (3/2) v1A |
[11] |
| las elevo al cuadrado la [10] y la [11] y aparecen |
| |
v2A² = (1/4) v1A² |
[12] |
| |
v2B² = (9/4) v1A² |
[13] |
| Todavía falta la subida de cada bola desde el evento 1 (justo después del choque) hasta el F (la altura máxima que alcanzan). Son ascensos conservativos así que... |
| |
½ mA v2A² = mA g hFA |
|
| |
½ mB v2B² = mB g hFB |
|
| Simplificando un poco la cosa: |
|
| |
hFA = v2A² / 2 g |
[14] |
| |
hFB = v2B² / 2 g |
[15] |
| Meto la [12] en la [14], y la [13] en la [15]. |
| |
hFA = (1/4) v1A² / 2 g |
[16] |
| |
hFB = (9/4) v1A² / 2 g |
[17] |
| Ya llegamos. Reemplazo la [1] en la [16] y en la [17] y aparece la respuesta |
|
|
|
| |
hFA = (1/4) h0A |
|
| |
hFB = (9/4) h0A |
respuesta d) |
|
|
|
| Bueno, como viste, este problema tiene 90% de álgebra y 10% de física. Pero ya que nos tomamos tanto trabajo... hagamos una linda discusión y vas a ver que valió la pena. Hay más física esperándote. |
|
|
DISCUSION: Por simple curiosidad... ¿cuánto te parece que debe valer la energía mecánica final del sistema? ¡La misma que la inicial, claro! ¡Si todas las transformaciones que hubo fueron conservativas! Y la energía mecánica final es puramente potencial, porque en F los cuerpos tienen velocidad cero. Entonces
EMF = EPFA + EPFB = mA g hFA + mB g hFB
= mA g (1/4) h0A + mB g (9/4) h0A
y reemplazando la relación de masas mB = (1/3) mA
= mA g (1/4) h0A + (1/3) mA g (9/4) h0A
= mA g (1/4) h0A + mA g (3/4) h0A = mA g h0A = EM0 !!!
|
|
 |
DESAFIO: El sistema evoluciona de esta manera: Las bolas vuelven a bajar y vuelven a chocar... ¡justo en el punto más bajo de la trayectoria! Se trata de un encuentro formidable, una cita espectacular. En ese encuentro, en ese nuevo choque la bola B empuja a la A, transfiriéndole su energia, de forma tal que la B se queda detenida y la A gana velocidad para poder alcanzar la altura inicial... y así sigue eternamente.
Contarlo es divertido, ¡y demostrarlo es súper sencillo! Ese es el desafío: me alcanza con que demuestres que aunque las dos bolas salieron con distintas velocidades y alcanzaron distintas alturas... se van a volver a encontrar en la misma en la posición que chocaron antes, al que llegan en el mismo e increíble instante. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Dijo Albert Einstein: "toy cansado". Última actualización nov-06. Buenos Aires, Argentina. |
|
|
|

