NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, choque plástico bidimensional)
|
|

|
3.19- Se recubre el borde de dos discos de
hockey sobre hielo con una cinta VELCRO, de
modo que los dos discos se adhieran al chocar.
Inicialmente el disco 1 tiene una velocidad de
8 m/s en la dirección de las x positivas, y el disco
2 tiene una velocidad de 10 m/s formando un ángulo
de 120º respecto a la dirección de las x positivas.
Los dos discos chocan y se pegan. ¿Qué fracción de la energía cinética total inicial
se disipa en la colisión?
a) 20 % b) 40 % c) 74 %
d) 99 %
c) 53% d) 9 %
|
¿Hiciste el problema 3.9?, era un auto y un camión que chocaban plásticamente. En nuestra jerga clasificatoria lo llamamos choque plástico en dos dimensiones. Bien, este pertenece al mismo grupo. Tiene una pequeña dificultad adicional, pequeñisima, y consiste que en el 3.9 los cuerpos que chocaban se acercaban al choque ortogonalmente (con perdón de la palabra), o sea en un ángulo de 90 grados. Eso simplificaba bastante la resolución del ejercicio. En éste los cuerpos -que esta vez no llevan ocupantes- llegan al encuentro en un ángulo diferente.
Ahora, bien, el enunciado sugiere (veladamente) un SR, y le vamos a hacer caso. |
|
|
 |
Siendo idénticas las masas de los cuerpos me voy a ahorrar los subíndices. Más aún, en cuanto planteo la ecuación de conservación de la cantidad de movimiento total
ΔPT = 0
me doy cuenta de que puedo cancelar las masas, mirá:
m v1 + m v2 = 2 m vF
v1 + v2 = 2 vF
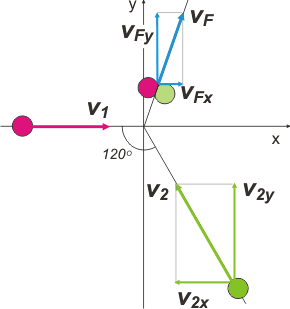
pero no nos olvidemos que esta es una relación vectorial y que estos vectores no son codireccionales. Vamos a tener que descomponer los vectores en dos direcciones. |
|
|
|
v1x + v2x = 2 vFx [1]
v1y + v2y = 2 vFy [2]
Con v1 no hay problema ya que su dirección coincide con x, de modo que
v1x = v1 = 8 m/s
v1y = 0
Con v2 hay apenas un poco más de complicación. Pero si seguís atentamente la construcción geométrica, vas a estar de acuerdo conmigo en que
v2x = — v2 cos 600 = — 5 m/s
v2y = v2 sen 600 = 8,66 m/s
Ahora podemos volver a las ecuaciones [1] y [2] que quedaron esperando
vFx = 1,5 m/s
vFy = 4,33 m/s
La velocidad final de conjunto pegado por el velcro la obtengo por pitágoras, ya que
vFx2 = vFx2 + vFy²
vFx2 = 21 (m/s)²
vFx = 4,6 m/s
y forma un ángulo con la dirección positiva de x cuya tangente es igual a vFy / vFx, y eso es aproximadamente 71 grados. Pero vamos a la pregunta del enunciado, nos pide averiguar qué fracción de energía cinética se pierde (se absorbe el velcro). Para eso tenemos que conocer la energía antes del choque y compararla con la energía después del choque. No podemos conocer ninguna de las dos, ya que no conocemos el valor de las masas, pero como no están pidiendo una fracción, si sabemos plantear esa fracción, las masas se cancelarán y se acabará el problema. Probemos.
ECF = ½ (2m) vF² = m vF²
EC0 = ½ m v1² + ½ m v2² = ½ m (v1² + v2²)
Ahora los dividimos miembro a miembro: |
|
|
| |
|
ECF |
= |
m vF² |
|
|
|
| EC0 |
½ m (v1² + v2²) |
|
|
|
| |
|
ECF |
= |
2 vF² |
|
|
|
| EC0 |
v1² + v2² |
|
|
|
| |
|
ECF |
= |
2 (4,6 m/s)² |
|
|
|
| EC0 |
(8 m/s)² + (10 m/s)² |
|
|
|
|
|
|
| Eso es la energía que quedó, un 25 %, luego, lo que falta es la energía que se disipó. |
|
|
| |
Edis (%) = 74 % |
respuesta c) |
|
|
|
| DESAFIO: Supongamos que los discos llegan al encuentro con una pequeña diferencia de tiempo de modo que el choque no es frontal, pero aún así las cintas de velcro funcionan y los discos quedan enganchados. ¿Cómo evoluciona el sistema? ¿qué le pasa al conjunto de discos unidos? ¿Qué resultados de este problema cambian? |
|  |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Iban todos en un auto convertible, chocaron y Vertible se murió. Última actualización dic-06. Buenos Aires, Argentina. |
|
|

