 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, choque plástico, energía mecánica)
|
|

|
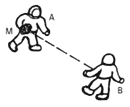
| 3.11- Dos astronautas, A y B, de 120 kg cada
uno, se encuentran en reposo cerca de su cápsula,
que constituye su sistema de referencia. A tiene
en sus manos una muestra rocosa M de 30 kg,
y se la envía a B para que la examine. La muestra
es arrojada por A con una velocidad de
0,4 m/s respecto a la cápsula. |
 |
|
| a- |
Determinar la velocidad que tendrá A luego
de arrojar la muestra (en módulo y sentido) y la
energía que se ha transformado en energía cinética
en ese proceso.
|
| b- |
Hallar la velocidad de B luego de recibir la
muestra, y la energía cinética perdida en ese proceso.
|
| c- |
Determinar los impulsos recibidos por M en
el lanzamiento, y en su choque contra B. |
|
|
|
Para responder el ítem a) conviene que nos olvidemos del segundo astronauta: se trata de un negocio entre el astronauta A y su piedra. La expulsión de la piedra es lo mismo que un choque plástico, pero al revés. En el choque plástico dos cuerpos se encuentran y se funden en uno. En nuestro caso son dos cuerpos que se separan. Pero la ecuación es la misma... hay un antes y un después, pero eso lo sabemos nosotros... para la ecuación es indistinto si antes estaban separados y después juntos, o viceversa.
vAp (mA + mp) = mA vA + mp vp
Pero la velocidad del astronauta con la piedra, antes de arrojarla, vAp, es nula (el enunciado lo dice: se encuentran en reposo), de modo que el primer miembro vale cero.
0 = mA vA + mp vp
0 = 120 kg . vA + 30 kg . 0,4 m/s
|
|
|
|
|
|
El signo menos indica que se moverá en sentido opuesto a la piedra. La variación de energía cinética es fácil de hallar: es la resta entre la energía que tenían después de arrojar la piedra menos la que tenían antes (nula, porque estaban en reposo).
ΔEc1 = Ecd1 — Eca1
ΔEc1 = ½ mA vA² + ½ mp vp² — 0
ΔEc1 = ½ 120 kg .( 0,1 m/s)² + ½ 30 kg . ( 0,4 m/s)²
|
|
|
|
|
|
Ahora la roca llega al astronauta B que la atrapa y se queda con ella.
mB vB + mp vp= vBp (mB + mp)
No te olvides que el astronauta B espera a la piedra en reposo ( vB = 0). Entonces:
mp vp= vBp (mB + mp)
30 kg . 0,4 m/s = vBp (120 kg + 30 kg)
|
|
|
|
|
|
Seguro que la atajada tuvo un costo energético. Calculemos:
ΔEc2 = Ecd2 — Eca2
ΔEc2 = ½ (mB + mp) vBp² — ½ mp vp²
ΔEc2 = ½ 150 kg (0,08 m/s )² — ½ 30 kg . (0,4 m/s)²
|
|
|
|
|
|
El impulso que el astronauta A le imprime a la piedra es igual a la diferencia de cantidad de movimiento de la piedra:
IAp = Δpp1
IAp = ppd1 — ppa1
IAp = mp vp — 0
IAp = 30 kg . 0,4 m/s
|
|
|
|
|
|
Y el impulso en la atajada es igual a la variación de cantidad de movimiento de la piedra antes y después de la atajada.
IBp = Δpp2
IBp = ppd2 — ppa2
IBp = mp vBp — mp vp
IBp = 30 kg . 0,08 m/s — 30 kg . 0,4 m/s
|
|
|
|
|
|
| |
|
|
| DESAFIO: ¿Cuánto vale la cantidad de movimiento total del sistema formado por los dos astronautas y la piedra? ¿Cuánto la variación de energía cinética del sistema? ¿De dónde salió esa energía? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jun-08. Buenos Aires, Argentina. Mantener lejos del alcance de los físicos. |
|
|
|

