home  | más de trabajo y energía | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, choque plástico, energía mecánica)

  

3.10- En los extremos de la pista de la figura hay dos carritos, que pueden moverse con rozamiento despreciable. Al carrito A, de 3 kg, se lo tiene en reposo, a 1,8 m por encima del tramo horizontal. El carrito B, de 2 kg, es mantenido en reposo contra un resorte de constante elástica 1800 N/m, acortándolo 40 cm a partir de su estado sin deformación. Se liberan ambos, y corren por la pista de modo que se encuentran en el tramo
horizontal. Allí se enganchan y prosiguen juntos.
                          
  a- Determinar con qué velocidad se moverán después de engancharse.
b- Si primero se dirigen hacia el resorte, hallar qué longitud máxima lo desplazarán; en caso contrario, a qué altura máxima llegarán sobre la rampa.
c- Hallar el impulso recibido por B, y la variación de energía cinética que experimenta:
         - debido al resorte
         - debido a su choque con A.
   
Este es uno de esos típicos problemas de física que antes de empezar a resolver tenés que tener seguridad plena de que ni el amor de tu vida, ni el de esta semana, te va a interrumpir. Es largo. Vamos a ponerle nombre a cada evento para poder compararlos a través de alguna ley de conservación.    
Llamé 0 a la situación inicial, los dos carritos están llenos de energía, pero todavía no los sueltan.
1. Llegan abajo con mucha velocidad, o sea cada uno transformó su energía inicial en cinética. Todavía no chocaron.

Voy a empezar con el carrito A, su proceso 0-1. Es una bajada conservativa, ya que no hay rozamiento ni tracciones.

EMA0 = EMA1

mA g h0A = ½ mA v1A²

g h0A = ½ v1A²

v1A = (2 g h0A)½

Sigo con el carrito B, su proceso 0-1. También es conservativo, ya que no hay rozamiento ni tracciones.

EMB0 = EMB1

½ k Δx0² = ½ mB v1B²

v1B = (k Δx0² / mB)½

Si tenés ganas de ir haciendo números, estás en tu derecho... a mí los números me dan un poco de alergia. Me alcanza con saber que tanto a v1A como v1B los tenemos.

1. Están por chocar

2. Ahí chocan. Y quedan pegados, o enganchados, es lo mismo. A partir de ahí se comportarán como un cuerpo único cuya masa será la suma de las masas individuales.

3. Después del choque podrían ocurrir tres cosas. O que el conjunto se quede detenido, o que salga hacia la izquierda o que salga hacia la derecha. Veremos veremos después lo sabremos.

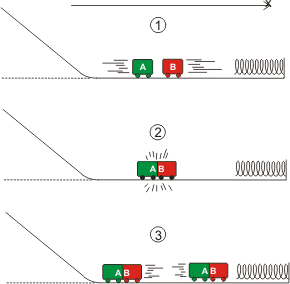Resolvamos este choque. Sabés que no tenemos ecuaciones que describan el choque, pero tenemos una ley de conservación que permite vincular un instante antes del choque con un instante después. Justamente el 1 con el 3.

Se trata de la ley de conservación de la cantidad total de movimiento. Es una relación vectorial y por suerte las velocidades son unidireccionales. Pero hay que asignar un SR que le dará signo a las velocidades. Justamente, analizando el signo de la velocidad del conjunto sabremos para qué lado sale.

mA v1A + mB v1B = v3 (mA + mB)

mA (2 g h0A)½ — mB (k Δx0² / mB)½ = v3 (mA + mB)

v3 = mA (2 g h0A)½ — mB (k Δx0² / mB)½ / (mA + mB)
  v3 = — 1,2 m/s como es negativo se dirigen hacia la rampa
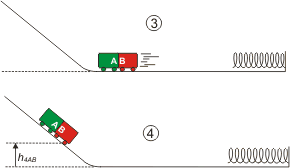
4. Si hubieran salido para la derecha habrían terminado comprimiendo un poco al resorte, pero salieron para la izquierda de modo que terminarán subiendo cierta altura por la rampa.
   
Entonces comparo la situación 3 con la 4 correcta, o sea arriba de la rampa, por energía mecánica para el cuerpo del conjunto unido.

EMAB3 = EMAB4

½ (mA + mB) v3² = (mA + mB) g h4

½ v3² = g h4

h4 = v3² /2 g

   
  h4 = 0,072 m  
   

Ojo, a partir de ahora sólo me ocupo de B, por pedido del enunciado. El impulso es igual a la variación de la cantidad de movimiento, entonces

I01B = mB v1B — mB v0B

I01B = mB v1B

    
  I01B = — 24 Ns  
   

Ahora la energía cinética. La variación de energía cinética debe ser positiva, ya que antes de ser impulsado estaba quieto y después no.

ΔEc01B = ½ mB v1B2 — ½ mB v0B²

ΔEc01B = ½ mB v1B2

   
  ΔEc01B = 144 J  
   

Ahora los mismos cálculos pero para el choque con el carrito A.

I13B = mB v3B — mB v1B

fijate que no importa que haya quedado unido a A, para calcular el impulso que recibió (lo mismo su energía) mantiene su individualidad, pobrecito.

   
  I13B = 21,6 Ns  
   

Finalmente la variación de energía cinética que sufre B debido al choque será

ΔEc13B = ½ mB v3B2 — ½ mB v1B²

   
  ΔEc13B = — 142,56 J  
   
DESAFIO: Modificar un dato cualquiera para que el resultado del problema sea que el conjunto comprime al resorte en 40 cm, lo mismo que estaba acortado al principio... ¿será posible?   Ricardo Cabrera
Algunos derechos reservados. Se permite su reproducción citando la fuente. Se agradece la lectura atenta de Julia Barboza y de Martín Triay que detectaron sendas erratas. Última actualización nov-06. Buenos Aires, Argentina.