3.5- Una bala de fusil de 40 g que se mueve a 300 m/s choca contra un bloque de madera de 2 kg que descansa en reposo sobre una superficie
horizontal. El proyectil atraviesa el bloque, y sale del mismo con una velocidad de 100 m/s. Sabiendo que el coeficiente de rozamiento entre
el bloque y el piso es μ_d= 0,2, hallar a qué distancia de su posición inicial se detendrá.

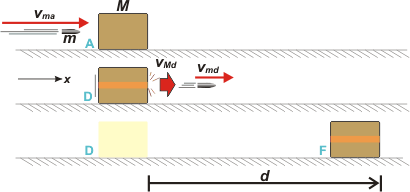
Hay cierta dificultad en este enunciado, y es comprensible que deje una cantidad de gente afuera. Mirá es así: cuando la bala atraviesa el bloque, eso es un choque, lo planteás y lo resolvés como un choque común y silvestre. Después del choque los cuerpos (bala y bloque) salen despedidos con diferentes velocidades. La bala se pierde. El bloque desliza con rozamiento y se frena. Vamos a verlo en un esquemita que te preparé en tres etapas.

¿Te cierra ahora? En ese caso te imaginarás que es un problema sencillísimo. Primero planteamos y resolvemos el choque (no dejes de leer la discusión del choque). Después, pérdida de energía por rozamiento. Y ya.

Te voy a aclarar las iniciales que usé. m es la masa de la bala, es dato. M es la masa del bloque, es dato. v_ma es la velocidad de la bala antes del choque, es dato. v_Ma es la velocidad del bloque antes del choque, es dato y es cero. v_md es la velocidad de la bala después del choque, y es dato. Y v_Md es la velocidad del bloque después del choque y es nuestra primera incógnita. Ahí va el choque.

m v_ma + M v_Ma = m v_md + M v_Md

m v_ma = m v_md + M v_Md

M v_Md = m v_ma — m v_md

v_Md = ( v_ma — v_md ) m / M

v_Md = 4 m/s

Ahora, nos olvidamos de la bala y nos concentramos en el bloque. En el tramo DF pierde toda la energía por el rozamiento. La ecuación que describe esa pérdida es la que dice que el trabajo de las fuerzas no conservativas es igual a la variación de energía mecánica.

W_FncDF = ΔE_MDF

W_RozDF = E_MF — E_MD

— μ_d M g d = — ½ M v_Md²

Bueno, yo te había avisado que era fácil.

DISCUSION: Lo más interesante que tiene este ejercicio es que te muestra un choque interesante. Es un choque raro, no te lo voy a negar, pero tiene la virtud de señalarte la existencia de los choques que no son absolutamente elásticos ni absolutamente plásticos.

Los absolutamente elásticos son aquellos en los que durante el choque no se pierde nada de energía. Los absolutamente plásticos ocurren cuando los cuerpos quedan pegados o unidos después del choque. Son dos extremos de un abanico enorme de posibilidades que representa el 99,99 % de los choques reales. No te quedes sólo con los dos extremos, quedate con la realidad.

No hay uniformidad de criterio en cómo nombrar los tipos de choque. Hay quien llama a los intermedios inelásticos. También hay quien llama plástico a todo aquel que no sea perfectamente elástico sin importar que hayan quedado o no unidos los cuerpos.