NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
2.22- Un hombre empuja un paquete de 10 kg
a lo largo de un plano inclinado con rozamiento
de 2 m de longitud. Para ello le aplica una fuerza
constante y paralela al plano; en consecuencia el
paquete, que estaba inicialmente en reposo en el
punto A, abandona el plano con una velocidad
de 1,8 m/s, e impacta en el punto C.
|
a - Realice los diagramas de cuerpo libre para
los tramos AB y BC.
b - Hallar el trabajo de la fuerza que aplica el
hombre.
c - Calcule el módulo de la velocidad del paquete
al llegar al piso, y su altura máxima, utilizando
consideraciones energéticas.
d - Calcule el trabajo realizado por la fuerza peso
en los tramos AB, BC, y AC.
|
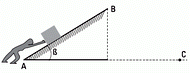 |
| μ = 0,1 β = 37° |
|
Este es uno de esos típicos ejercicios en los que el único remedio es arremangarte... proveerte un buen mate y un buen termo... y resignarte a no hablar por teléfono durante una hora. Así es la vida del estudiante. Pero no te quejes... el ejercicio es fácil. Vamos con los diagramas. |
|
|
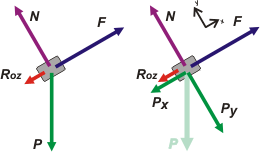 |
Como ves, en el tramo recto las fuerzas que actúan son: la fuerza peso, P, la fuerza de apoyo con el plano, N, la fuerza de rozamiento, Roz, y la fuerza que hace el hombre, F.
Si tenés ganas de reparar en dos detalles. Fijate que la fuerza F debe ser mayor que la suma de la componente del peso paralela al plano (tenés que descomponer el peso), más el rozamiento. Sólo así podría acelerar hacia arriba. |
|
|
|
| El otro detalle es que la componente del peso perpendicular al plano debe ser igual a N. Sólo así se mantendría apoyado sobre el plano. |
|
|
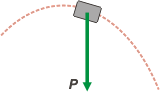 |
En el tramo libre (un vuelo en tiro oblicuo desde B hasta C) la única fuerza que actúa sobre el cuerpo es la fuerza peso, P, como ocurre en todos los movimientos libres (ésa es la definición). |
|
|
|
Ahora vamos a hallar el trabajo de la fuerza que aplica el man, WF. No hay un único camino para hallarlo, pero por los datos que nos brindan, me parece bastante directo éste:
WRes = ΔEC = ½ m vB² = ½ 10 kg . (1,8 m/s)²
WRes = 16,2 J
El trabajo de la resultante es igual a la suma de los trabajos de las tres fuerzas que trabajan:
WRes = WRoz + WPx + WF
Los trabajos de la componente x del peso y del rozamiento los tenés acá (no me voy a explayar demasiado en esto porque ya lo trabajaste de sobra en dinámica).
WRoz = μ . m . g . cos β . 2 m . cos 180º = — 16 J
WPx = m . g . sen β . 2 m . cos 180º = — 120 J
Reemplazando estos valores en la suma del trabajo de la resultante, despejo, y... |
|
|
|
|
|
Ahora vamos a veriguar la energía mecánica en los puntos B, M y C, donde M es la posición de altura máxima. De más está decir que en todos esos puntos la energía mecánica valdrá lo mismo, ya que durante el vuelo libre no hay ninguna fuerza no-conservativa actuando.
EMB = EMM = EMC = EPB + ECB
La cinética es muy fácil, porque nos dan la velocidad. Pero para conocer la potencial hay que saber a qué altura se halla y eso lo resolvemos aplicando un poquito de trigonometría al trianguloto cuya hipotenusa es el plano inclinado por el que subió el cuerpo.
ECB = ½ m vB² = 16,2 J
EPB = m . g . hB = m . g . 2 m . sen β = 120 J
EMB = EMM = EMC = 136,2 J
Esa energía se convierte totalmente en cinética al llegar a C.
EMC = ½ m vc²
vc² = 2 . 136,2 J / 10 kg
|
|
|
|
|
|
En el punto M, en cambio, una parte de la energía cinética se conserva, ya que pese a que el cuerpo deja de subir, no deja de avanzar. Si en el momento de la partida del vuelo la velocidad valía: vB = 1,8 m/s. Entonces la componente horizontal de esa velocidad (que no perderá durante el vuelo) valdrá:
vBx = vB . cos β = 1,8 m/s . 0,8 = 1,44 m/s
Y la energía cinética de M valdrá:
ECM = ½ m vM² = 10,4 J
Por lo tanto la energía potencial de M valdrá:
EPM = EMM — ECM = 136,2 J — 10,4 J = 125,8 J
Que se corresponde con una altura de... |
|
|
|
|
|
Por último los trabajos de la fuerza peso... pan comido...
WPAB = — ΔEPAB , WPBC = — ΔEPBC , WPAC = — ΔEPAC
Teniendo en cuenta que las energías potenciales de los puntos A, B y C valen:
EPA = m . g . hA = 0 J
EPB = m . g . hB = 120 J
EPC = m . g . hC = 0 J
|
|
si además de aprender Física te divertiste, no dejes de leer mi novela policial
Por las barbas de Juno |
| |
WPAB = — 120 J
WPBC = 120 J
WPAC = 0 J |
|
|
|
|
| |
|
|
 |
| DESAFIO: Hacete un gráfico de energías en función del tiempo, indicando los instantes de A, B, M y C. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco el envío de una errata a Emanuel Muiño. Última actualización nov-08. Buenos Aires, Argentina. |
|
|
|

