NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
 |
2.19- Un resorte de masa despreciable está
apoyado contra el piso, con su eje vertical. Al colocarle
encima una caja, el equilibrio se consigue
con el resorte comprimido 10 cm por debajo de
su posición original. ¿Desde qué altura por encima
de su posición inicial deberá dejarse caer la
caja sobre él, para que llegue a comprimirse hasta
30 cm por debajo de la misma? Hallar también
la velocidad con que pasará por la posición de
equilibrio, y hasta qué altura ascenderá luego del
rebote, si se desprecian los rozamientos. |
|
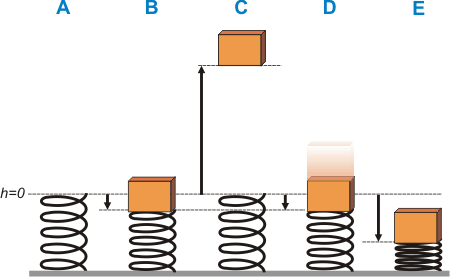
Siempre, en los problemas de leyes de conservación se comparan situaciones, estados, eventos, o lo que quieras... pero se compara de a dos. Y en casi todos los problemas, también, se habla de muchas situaciones... muchas más que dos. De modo que para entender cuáles dos estamos comparando (de a una comparación por vez) hay que ponerle nombre a todas las situaciones mencionadas en el enunciado. Fijate si te cierra este esquemita que hice para aclarar la descripción, y de paso, ponerle nombre a cada situación:
|
|
|
|
Tal vez notaste que falta la última situación mencionada en el problema: "hasta dónde llega cuando rebota", en efecto no la puse, soy caprichoso.
La situación A te muestra al resorte apoyado en el piso tal como lo compramos en la ferretería. Ahí su compresión vale cero, no esta ni comprimido ni estirado. Arbitrariamente alegí la posición de su espira superior como nivel cero de alturas. Podría haber elegido otro cualquiera, por ejemplo el piso. Preferí ése porque las compresiones están definidas desde ese nivel y eso me desliga de la longitud del resorte, sobre el cual el problema nada dice. El único recaudo que hay que tomar cuando se define un sistema de alturas es que todo lo que esté debajo del nivel cero debe tener una altura negativa. Por ejemplo, la altura del cuerpo en la situación B es –10 cm o sea –0,1 m.
Entre la situación A y B no hay nada que comparar energéticamente. A la situación B se llega apoyando suavemente la caja y se hace simplemente para que puedas acceder a alguna información extra. Te lo muestro en un DCL de la situación B. |
|
|
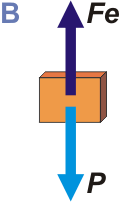 |
El enunciado te dice claramente que en B la caja se halla en equilibrio, eso te permite afirmar que
Fe = P
o sea
k . ΔxB = m . g
Ahora ya podés considerar dato la constante elástica, que te estaba faltando (no la calcules, por favor, combatí tu reemplacismo, que es dañino). Dejalo así:
k = m . g / ΔxB
|
|
|
|
Ahora sí, empecemos con las comparaciones energéticas. Qué eventos comparar, eso lo vas a adquirir con la experiencia. Podés comparar cualquier par de eventos, si no hallás las incógnitas, probás con otro par... y así.
Voy a comparar primero C con E.
WFncCE = ΔEMCE
No hay ninguna fuerza no-conservativa actuando, de modo que el primer miembro vale cero y puedo escribir:
EMC = EME
por definición de lo que es energía mecánica
ECC + EPGC + EPEC = ECE + EPGE + EPEE
½ m vC² + m g hC + ½ k ΔxC² = ½ m vE² + m g hE + ½ k ΔxE²
hay varias cosas que valen cero. Por ejemplo ECC = 0 (dice deberá dejarse caer) eso significa vC = 0. También es cero la velocidad en E ya que se trata de la compresión máxima lograda al dejar caer la caja desde C. Por último, la energía elástica en C también vale cero... si ni siquiera están en contacto la caja y el resorte... cómo iba a poder conferirle energía...
m g hC = m g hE + ½ k ΔxE²
hE es igual a ΔxE (pero negativo, no te olvides) de modo que la única incógnita ahí es hC, sólo hay que despejarla.
hC = — ΔxE + ½ k ΔxE² / m g
acá reemplazo k (viste que no era necesario calcularla)
hC = — ΔxE + ½ ΔxE² / ΔxB
|
|
|
|
|
|
Para saber con qué velocidad pasa por D, puedo comparar C con D o D con E. Siempre es preferible no utilizar datos que uno halló en el mismo ejercicio, es obvio por qué. Así que voy a comparar energéticamente D con E.
EMD = EME
ECD + EPGD + EPED = ECE + EPGE + EPEE
½ m vD² + m g hD + ½ k ΔxD² = ½ m vE² + m g hE + ½ k ΔxE²
tiro un término nulo
½ m vD² + m g hD + ½ k ΔxD² = m g hE + ½ k ΔxE²
hD es igual a ΔxB, es igual a ΔxD (pero negativo, no te olvides) de modo que la única incógnita ahí es vD, sólo hay que despejarla.
vD= (— 2 g ΔxE + 2 g ΔxB — g ΔxB + g ΔxE²/ ΔxB)½
vD= (— 2 g ΔxE + g ΔxB + g ΔxE²/ ΔxB)½
|
|
X 1/2
es lo mismo que
raíz cuadrada de X
(lo escibo de esa manera para no tener que reemplazar el texto por una imagen) |
|
|
|
|
| La altura a la que llegará después de rebotar no es difícil de predecir, habida cuenta que despreciamos todas las fuerzas no-conservativas que puedieran actuar. |
|
 |
| DESAFIO: ¿Con qué velocidad pasa por el nivel cero? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
|

