NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
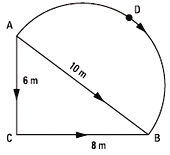
| 2.3- Determinar el trabajo que realiza la fuerza
de rozamiento que actúa sobre un cuerpo de
20 kg, al desplazarlo desde el punto A hasta el B
del esquema (vista desde arriba de las trayectorias)
tirando de él con una cuerda paralelamente
a la superficie horizontal donde está apoyado, si
el coeficiente respectivo es μd= 0,4: |
a- Por el camino directo (1)
b- Pasando previamente por C (Camino 2)
c- Por la semicircunferencia ADB (Camino 3)
d- ¿Es conservativa la fuerza de rozamiento?
e- Hallar el trabajo que realiza la fuerza que
ejerce la cuerda en cada caso, suponiendo que el
objeto se desplaza con velocidad de módulo
constante. |
 |
|
En la sección de energía no hay otro ejercicio más pavo. Sin embargo los estudiantes lo miran de lejos, de reojo... y se alejan como de un bicho sarnoso. ¿Hiciste ése?, les pregunto. No profe... es muy complicado: un plano inclinado, una colina... ¿Un quéee? Andá y volvé a leer el enunciado, plano inclinado... ¡y prestá atención a lo que dice el enunciado!
Todo transcurre en un plano horizontal en el piso: el esquema que acompaña al enunciado representa una vista aérea, una vista cenital, como si fuera de Google Earth. Te lo voy representar de nuevo para que te quede más claro: |
|
|
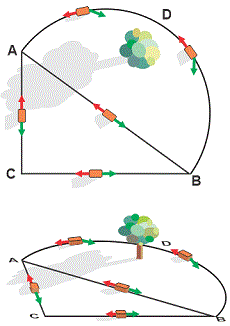 |
El de arriba es el mismo esquema que el del enunciado solo que inventé un cuerpo cualquiera -una caja- y la coloqué en algún momento de cada viaje; y además le dibujé un arbolito y una sombrita para darle más profundidad y realismo a la perspectiva.
Por si fuera poco, volví a representarlo en una perspectiva oblicua para que no te quepa duda qué es lo que estás viendo y qué lo que te están pidiendo. ¿Estamos?
La fuerza de rozamiento la representé con una flechita roja y la fuerza que realiza la cuerda con una verde. La de rozamiento es constante ya que se trata de un rozamiento dinámico en el que la fuerza de contacto (N) no cambia. Ahora: si entendiste cómo funciona ésto, estarás de acuerdo en que la fuerza de rozamiento forma permanentemente un ángulo de 180º con el desplazamiento; de modo que...
|
|
|
|
La segunda ley de la dinámica nos asegura que la fuerza que comprime la superficie del objeto con el piso, es igual a su peso: 200 N, de modo que la fuerza de rozamiento vale:
Roz = μ . P = 0,4 . 200 N = 80 N
Calcular sus trabajos es juego de niños (de 6 a 9 años y medio).
WRozAB = Roz ΔxAB cos 180º
WRozAB = — 80 N . 10 m
|
|
|
|
|
|
WRozACB = WRozAC + WRozCB =
WRozACB = Roz ΔxAC cos 180º + Roz ΔxCB cos 180º =
WRozACB = — 80 N . 6 m — 80 N . 8 m = |
|
|
|
| |
Para el cálculo por la trayectoria curva alcanza con conocer su extensión, porque el resto de las variables que interesan para el cálculo del trabajo no cambia: el ángulo de la fuerza con el desplazamiento es siempre el mismo (lo dibujé en dos posiciones diferentes en los esquemas, para que te saques las dudas). El hecho de que el desplazamiento sea curvilíneo tampoco es problema. Eso lo discuto al final, ¿ok?
El largo de una semicircunferencia es igual a 3,14 veces el radio de la circunferencia. Y eso en nuestro caso da: 15,7 metros.
WRozADB = Roz ΔsADB cos 180º
WRozADB = — 80 N . 15,7 m
|
|
|
|
|
|
Vos sabés casi religiosamente que la fuerza de rozamiento no es conservativa. De hecho es una de las fuerzas no-conservativas arquetípicas... que siempre le están quitando energía mecánica a todos los sistemas donde aparecen. Pero la idea acá es que repares en lo siguiente. Por tres caminos diferentes el objeto viajó desde el punto A hasta el B. El trabajo del rozamiento en las tres transformaciones fue diferente, ergo, no puede tratarse de una fuerza conservativa.
Se trata de uno de los criterios utilizados para discriminar entre los tipos de fuerzas: conservativas o no-conservativas. Si el trabajo que realiza una fuerza entre dos estados diferentes de un objeto o sistema es el mismo, independientemente de cuál haya sido la trayectoria, entonces se trata de una fuerza conservativa. Y viceversa.
Con la última pregunta no pienso ayudarte mucho. La fuerza que arrastra al objeto debe ser igual y contraria al rozamiento en los casos a) y b). Eso lo garantiza el hecho de que el cuerpo se mueve a velocidad constante. En el caso c) esa fuerza debe tener una componente centrípeta para lograr el giro. Pero esa componente no realiza trabajo (es normal a la trayectoria). Por lo tanto, en los tres casos, sus trabajos deben ser iguales y contrarios a los que calculamos para el rozamiento. Obviamente se trata de otra fuerza no-conservativa, como casi todas las tracciones. |
|
|
| |
|
|
| DISCUSION: Si no tuviste inconveniente el averiguar el trabajo total desde A hasta B por la trayectoria quebrada, pasando por C, como una suma de los dos trabajos de los segmentos rectos de 6 y 8 metros... no deberías tener inconveniente en concebir el camino curvo de A a B pasando por D como una larga suma de pequeños segmentos rectos, tan pequeños que de lejos no parezca una sucesión de segmentos rectos sino una semicircunferencia suave y redonda. Como los segmentos deben ser muy pequeños la suma de todos ellos debe ser muy larga. Los científicos llamamos a esas largas sumas: integrales... y al mencionarlas, nos sentimos poderosos. |
|
 |
| DESAFIO: ¿Cuánto vale el trabajo de la fuerza peso en cada recorrido? |
|
| Algunos derechos reservados para evitar siniestros.
Se permite su reproducción citando la fuente. Se agradece a mi colega María Inés Braga Menéndez por el envío de una errata. Última actualización may-08. Buenos Aires, Argentina. |
|
|
|

