NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo)
|
|

|
 |
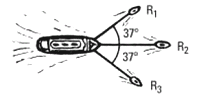
1.2- Tres remolcadores llevan un barco hacia
su dársena, tirando cada uno con una fuerza
constante de 3 x 105 N en un recorrido de 500 m,
como indica la figura. Si la fuerza de rozamiento
que ejerce el agua sobre el barco es de 1 x 105 N, determinar: |
|
a- La resultante de las fuerzas que actúan sobre
el barco.
b- El trabajo que realiza la fuerza resultante.
c- El trabajo que realiza cada una de las fuerzas
que actúan.
d- La suma de los trabajos calculados en c.
Comparar con el resultado del inciso b. |
 |
|
|
|
El primer requerimiento que nos hace el ejercicio es, simplemente, una suma de fuerzas que se resuelve del mismo modo que lo hicimos en estática y dinámica.
Voy a desestimar las fuerzas verticales: el peso del barco y el empuje que lo hace flotar. Ambas fuerzas -normales a la superficie- sabemos que no aportan a la resultante porque en el eje vertical la aceleración es nula: el barco no se hunde, ni levanta vuelo. |
|
|
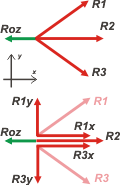 |
Las fuerzas no son colineales, de modo que voy a tener que descomponer alguna de ellas y reemplazarlas por sus componentes paralelas a los ejes de referencia. Tené en cuenta que:
R1x = R1 cos 37º, R1y = R1 sen 37º
R3x = R1 cos 37º, R3y = R3 sen 37º
El asunto queda así:
ΣFy = R1y — R3y = 0
ΣFx = R1x + R2 + R3x — Roz
|
|
|
|
La resultante, Res, será la composición de esas dos sumas... por suerte la componente y de la resultante también es nula (de lo cual ya te habías dado cuenta porque el barco no dobla, ni a babor ni a estribor) así que la resultante sólo tiene componente en x, y vale...
ΣFx = Res = R1x + R2 + R3x — Roz
ΣFx = Res = 2,4 x 105 N + 3 x 105 N + 2,4 x 105 N — 1 x 105 N
|
|
|
| |
Res = 6,8 x 105N |
respuesta a- |
|
|
|
Para calcular el trabajo de la resultante durante este desplazamiento podemos aprovechar que se trata de una fuerza constante y aplicar:
WF = F . Δx . cos α
Por lo que vimos, la fuerza resultante tiene la misma dirección y sentido que el desplazamiento, de modo que entre ambas (resultante y desplazamiento) forman un ángulo de 0º, su coseno vale 1.
WRes = Res . Δx . cos α
WRes = 6,8 x 105 N . 500 m . cos 0º
|
|
|
| |
WRes = 3,4 x 108 J |
respuesta b- |
|
|
|
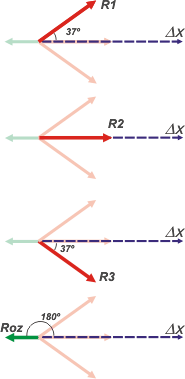 |
Los trabajos de cada una de las fuerzas, por separado, se obtienen de la misma manera que lo hice con la resultante:
WR1 = 3 x 105 N . 500 m . cos 37º = |
|
| WR2 = 3 x 105 N . 500 m . cos 0º = |
|
| WR3 = 3 x 105 N . 500 m . cos 37º = |
|
| WRoz = 105 N . 500 m . cos 180º = |
|
| Ahora, si sumamos los cuatro trabajos obtenidos, así, individualmente, nos da... |
|
|
|
| |
ΣWFi = 3,4 x 108 J |
respuesta d- |
|
|
|
No se trata de una casualidad de este ejercicio. Siempre ocurre que la suma de todos los trabajos de todas las fuerzas que actúan sobre un cuerpo, es igual al trabajo de la resultante. Si lo querés en una fórmula...
WRes = ΣWFi
|
|
 |
| |
|
| DESAFIO: Calculá en cuánto varía la energía cinética del barco en esos 500 m. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco la lectura atenta que hizo Adriana S. de Furrer, que detectó un error de cuentas y me envió la corrección en una carta amabilísima. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
|

