 |
NO ME SALEN
EJERCICIOS RESUELTOS DE BIOFÍSICA DEL CBC
(Leyes de conservación, trabajo) |
|
|

|
| |
 |
38)
a) Calcule, por consideraciones energéticas, la velocidad con la que debe lanzarse una
piedra verticalmente hacia arriba para que alcance una altura de 5 m. Desprecie el
rozamiento con el aire.
b) Si la piedra se lanzara oblicuamente, para que llegara a una altura máxima de 5 m,
¿debería arrojarse a mayor velocidad o la misma? Justifique su respuesta, también
en términos energéticos.
c) Realice los gráficos de energía cinética, potencial y mecánica en función de la altura. |
|
|
Este ejercicio, que podrías resolver fácilmente por consideraciones cinemáticas, vas a ver cuánto más fácil resulta por energía. |
|
|
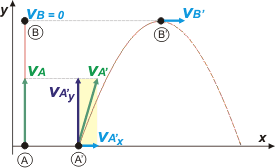 |
Me adelanté un poco e hice juntos los esquemas de las dos situaciones planteadas para que podamos sacarle provecho a la comparación.
La trayectoria vertical de la izquierda representa al tiro vertical narrado en el ítem a) y la parábola de la derecha, al lanzamiento oblicuo del ítem b). Fijate que ambos móviles alcanzan la misma altura: 5 metros. |
|
|
|
Vamos a los planteos energéticos. Empecemos con la piedra en vuelo vertical. Si se desprecia el rozamiento, no existe ninguna fuerza no-conservativa, por lo tanto:
EMA = EMB
En A la energía es puramente cinética y en B sólo potencial... porque en su punto más alto la velocidad vale cero.
ECA = EPB
½ m vA² = m g hB
vA² = 2 g hB
|
|
|
| |
|
|
Ahora el oblicuo. Tampoco hay fuerzas no-conservativas, así que:
EMA' = EMB'
En A' la energía es puramente cinética pero en B' hay potencial y cinética... porque en un tiro oblicuo la velocidad NUNCA se hace cero. Siempre conserva (al menos) la componente horizontal de la velocidad inicial que, además, es constante.
ECA = EPB + ECB
½ m vA'² = m g hB' + ½ m vB'²
vA'² = 2 g hB' + vB'²
|
|
|
|
|
|
Si comparás ambos resultados encontrarás fácilmente que vA' > vA.
Cada vez que en un examen pedimos un gráfico de energía en función de la posición -cosa bastante frecuente- queda un tendal de masacrados tirados por el aula. Un asco. |
|
|
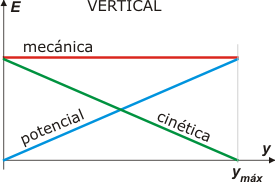 |
Miralos bien y no abandones el ejercicio hasta que los hayas entendido absolutamente. Las líneas rojas representan la energía mecánica. Las verdes la cinética. Y la azul, la potencial que, obviamente, es la misma para los dos movimientos ya que sólo depende de la altura (y).
Acá está el gráfico correspondiente al tiro vertical, más abajo aparece el del tiro oblicuo. |
|
|
|
La energía mecánica se mantiene constante (y su representación corresponde a una recta horizontal, la roja) ya que no actúa ninguna fuerza no-conservativa (acordate que se desprecia el rozamiento con el aire).
La energía potencial aumenta con la altura (EP = m g y) y aumenta en forma directamente proporcional, por lo tanto su representación se corresponde con una recta oblicua ascendente, que alcanza el valor de la energía mecánica en la altura máxima, porque en esa posición la energía cinética es nula.
La energía cinética tal vez no sea inmediato predecir su forma, pero si pensás que en todo momento es la resta entre la mecánica y la potencial, no le queda otra opción que tratarse de una recta oblicua descendente. |
|
|
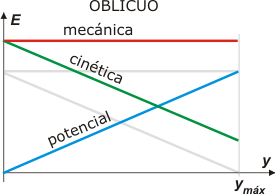 |
Acá tenés el correspondiente al tiro oblicuo. Si entendiste el anterior no tendrás inconveniente en interpretar correctamente este otro.
Para facilitarte la comparación dejé en gris suave el gráfico anterior.
La gran diferencia es que en el tiro oblicuo hay una componente de la velocidad (la componente de traslación horizontal) que se mantiene constante durante todo el vuelo lo cual aumenta -en un valor constante- las energías cinética y, por consiguiente, la mecánica. |
|
|
|
|
|
 |
| DESAFIO: First: demostrar analíticamente (partiendo de las ecuaciones de movimiento) que la energía cinética de un MRUV es una función lineal respecto de la posición. Second: (muy turro) hacer los gráficos energía-posición para ambos móviles en el viaje de vuelta. |
|
| |
|
| Algunos derechos reservados.
No se permite la comercialización de este magnífico material ni en pesos, ni dólares, ni yenes, ni oro, ni petróleo, ni soja, ni ningun otro comoditi, ni incomoditi. Se permite su reproducción citando la fuente. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
|

