 |
NO ME SALEN
EJERCICIOS RESUELTOS DE BIOFÍSICA DEL CBC
(Leyes de conservación, trabajo) |
|
|

|
| |
 |
37) El gráfico representa la componente
de la fuerza resultante en la dirección del
movimiento en función de la posición,
para un cuerpo de 5 kg, que
inicialmente se mueve a 0,2 m/s. |
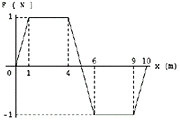 |
a) Calcule el trabajo de la fuerza
resultante para el desplazamiento del
primer metro, del segundo metro y de
los cinco primeros metros.
b) Determine en qué posición el cuerpo
tendrá el valor máximo de la energía
cinética y en cual el valor mínimo.
c) ¿En cuál o cuáles posiciones su
velocidad es de 1 m/seg? |
|
|
Este ejercicio tiene un 80 por ciento de ingenio y un 20 de Física. Por suerte ingenio es lo que te sobre. En cuanto a la Física, se trata de saber, simplemente que el área encerrada bajo la curva de un gráfico de fuerza en función del desplazamiento es equivalente al trabajo de esa fuerza. En particular, si esa fuerza es la resultante -como es el caso de este ejercicio- ese trabajo es igual a la variación de energía cinética.
Area = WRes
WRes = ΔEc
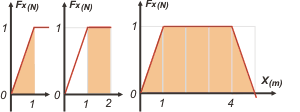
Te hice los tres grafiquitos donde podés ver las áreas integradas en los desplazamientos indicados. No te olvides que el segundo metro, por ejemplo, es el que empieza en la posición metro uno y termina en la posición metro dos. |
|
|
| |
W1erM = 0,5 J |
|
| |
|
|
| |
W2doM = 1 J |
|
| |
|
|
| |
W1eros5M = 4 J |
|
|
 |
|
|
|
El ítem b) es muy interesante; este sí, debo admitir, es pura Física. Las áreas que quedan del lado superior del eje de las x representan trabajos positivos, y las que quedan por debajo, trabajos negativos (esto es cierto mientras que el desplazamiento tenga el mismo sentido que el SR). Si el trabajo es positivo habrá aumento de energía cinética (y por lo tanto de velocidad). Si el trabajo es negativo habrá disminución de velocidad.
Para responder la pregunta debemos encontrar en qué posición se acumula más trabajo neto (positivo). Por ejemplo: en la posición 2 m la velocidad será mayor que en la posición 1 m, porque hasta los 2 m habíamos acumulado un trabajo de 1,5 J, contra 0,5 J del primer metro.
Siguiendo este razonamiento podés encontrar que la máxima velocidad la tendremos en xVmax = 5 m. A partir de esa posición el cuerpo recibe trabajo negativo por lo tanto su velocidad disminuye... ya no puede ser la máxima. Te dejo a vos que encuentres las posiciones de las velocidades mínimas. |
|
|
|
|
|
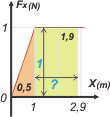
El ítem c) es totalmente de ingenio. Para saber en qué posición la velocidad va a valer 1 m/s, primero hay que saber que variación de energía cinética representa esa velocidad.
ΔEc(1m/s) = ½ 5 kg . (1 m/s)² — ½ 5 kg . (0,2 m/s)²
ΔEc(1m/s) = 2,4 J
|
|
|
De modo que cuando acumulemos -desde el principio- un trabajo igual a 2,4 J, la velocidad del cuerpo será 1 m/s. Eso se logra en dos posiciones, que podés encontrar calculando el área del rectángulo central.
0,5 J tenemos en el triangulito de inicio. para llegar a 2,4 J nos faltan 1,9 J. El rectángulo tiene una altura de 1... por lo tanto la base debe medir... |
 |
|
|
|
| |
|
 |
|
|
| |
|
| DESAFIO: Te dejo a vos resolver el siguiente enigma: hay otra posición, más allá de los 5 m, donde la velocidad vuelve a valer 1 m/s. ¿Cuál es esa posición y cómo se encuentra? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jul-08. Buenos Aires, Argentina. |
|
|

