 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Leyes de conservación, trabajo) |
|
|

|
| |
 |
32) Un esquiador de 80 kg se deja caer por una colina de 30 metros de altura, partiendo con
una velocidad inicial de 6 m/s. No se impulsa con los bastones y se puede despreciar el
rozamiento con la nieve y con el aire.
a) ¿Cuál es la energía mecánica inicial del esquiador? ¿Cambia este valor a lo largo
del recorrido? Justifique su respuesta analizando las fuerzas que actúan sobre el
esquiador. |
b) ¿Con qué velocidad llega el esquiador al pie de la colina?
c) ¿Qué debería hacer el esquiador para llegar al pie de la colina con una velocidad de
30 m/s? Justifique su respuesta sobre la base de consideraciones dinámicas y
energéticas (dé valores numéricos).
d) ¿Y si quisiera llegar con una velocidad de 15 m/s? |
|
|
Se trata de un sencillísimo ejercicio de aplicación del teorema del trabajo y la energía: la variación de energía mecánica es igual al trabajo de las fuerzas no-conservativas.
Que se aplica en la comparación energética entre dos situaciones, o dos estados, o dos lo que quieras... pero entre dos. |
|
|
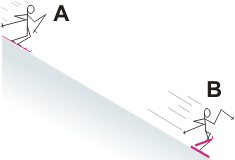 |
En este caso no hay mucho para elegir, será entre la salida y la llegada, que llamé A y B, respectivamente.
WFncAB = ΔEMAB
Eso que escribí se lee así: "el trabajo de las fuerzas no conservativas que actuaron entre A y B es igual a la variación de energía mecánica entre A y B". ¿Pudiste seguirlo? ¿Serás capaz de escribirlo igual de bien, sin olvidarte ningún subíndice, cuando te toque hacerlo a vos? |
|
|
|
Entre A y B no actuó ninguna fuerza no-conservativa: nadie empujó ni frenó, no hubo rozamiento... Luego, el primer miembro de la expresión vale cero.
0 = ΔEMAB
EMA = EMB
Esto ya responde parte de la pregunta b). Al no haber fuerzas no conservativas la energía mecánica se mantendrá durante todo el recorrido, y en especial en sus extremos A y B. Pero el enunciado nos pide que primero encontremos el valor de la energía mecánica en A. Para eso hay que fijar previamente un sistema de alturas: pongamos el cero en B.
EMA = ECA + EPA
EMA = ½ m vA² + m g hA
EMA = ½ 80 kg . 36 (m/s)² + 80 kg . 10 m/s² . 30 m
|
|
|
| |
|
|
Como te había dicho antes, la energía mecánica no cambiaba, entonces...
EMA = EMB = ½ m vB² + m g hB
EMB = ½ m vB²
25.440 J = ½ 80 kg . vB²
|
|
|
|
|
|
| |
|
|
Vamos a las dos preguntas finales. Te queda claro que el esquiador llega al fondo de la pista con una velocidad de vB = 25,2 m/s gracias a que durante la bajada no actúa ninguna fuerza no-conservativa, ¿ok?. Bueno... para llegar con una velocidad diferente a esa tendrá que rebuscárselas para que actúe una fuerza no-conservativa.
Para llegar con una velocidad mayor, 30 m/s, necesita un refuerzo de 10.560 J (hacé la cuenta). Una forma de lograrlo es enganchándose a un esquiador que va un poco adelante y tirando de él hacia atrás. Un modo menos peligroso y más corriente es impulsándose con los bastones. En este caso la energía necesaria saldrá del ATP hidrolizado en los músculos de los brazos.
Para llegar con una velocidad menor, 15 m/s, debe desprenderse de una cantidad de energía igual a 16.440 J (hacé la cuenta). Un modo de lograrlo es aumentar su masa comiendo las frutillas que va encontrando al avanzar. Otro método menos difícil es trabajar un poquito con la posición de los esquíes para que su rozamiento con la nieve deje de ser despreciable y se convierta en una fuerza de frenado efectiva. |
|
 |
| |
|
| DESAFIO: ¿Con qué velocidad llegaría un trencito integrado por 3 esquiadores tomados de la cintura, que salen con la misma velocidad que nuestro esquiador solitario, y tienen todos la misma masa? |
|
| Algunos derechos reservados.
Severísimas penas a quien orinase en un paso a nivel sobre la vía electrificada. Se permite su reproducción citando la fuente. Agradezco a Daniel Calisti por el envío de una errata. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
|

