 |
NO ME SALEN
APUNTES TEORICOS DE FÍSICA DEL CBC
(Leyes de conservación)
|
|

|
TRABAJO
Trabajo en física no es lo mismo que en el lenguaje coloquial. La diferencia fundamental es que en el lenguaje coloquial el trabajo es el producto de una persona, o de un animal o de un cuerpo. En física, trabajo es un atributo de una fuerza (voy a volver sobre esto, que es muy importante). Se suele representar con L o con W, y con un subíndice se aclara la fuerza a la que pertenece el trabajo expresado. Por ejemplo: WF (el trabajo de la fuerza F) o WRes (el trabajo de la fuerza Resultante) y así.
Para que haya un trabajo distinto de cero tiene que haber un desplazamiento del cuerpo sobre el que se ejerce la fuerza. Por ejemplo en la situación siguiente: |

|
|
|
Se define el trabajo de la siguiente manera (válida exclusivamente para fuerzas constantes): |
|
|
| |
WF = F . Δx . cos α |
¡sólo para fuerzas constantes! |
|
|
|
donde F es el módulo (la intensidad) de la fuerza, Δx es el módulo (el largo) del desplazamiento, y α es el ángulo que forman la fuerza con el desplazamiento.
El trabajo es un escalar, o sea un número (con su unidad) que nos indica cuánto aporta una fuerza a desplazar un cuerpo. El trabajo no tiene dirección ni sentido, no es un vector... es un escalar.
Las unidades en las que se miden los trabajos deben surgir del producto de las unidades en las que se miden las fuerzas, N, por las unidades en las que se miden los desplazamientos, m, por las unidades en las que se miden los cosenos (ninguna).
[W] = N . m = J (Joule)
por tratarse de una magnitud de suma importancia, la unidad con la que se mide recibe nombre propio, adoptado en honor al físico James Prescott Joule (1818-1889) del que ya te voy a volver a hablar.
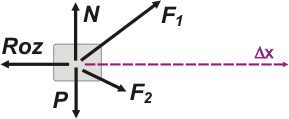
Supongamos que tenemos un cuerpo que se desplaza un cierto Δx sobre el que actúan varias fuerzas simultáneamente. |
|
 |
| James P. Joule |
|
|
|
Como el trabajo es un atributo (una característica, una magnitud) de las fuerzas yo podría plantear y calcular el trabajo de cada una de ellas; por ejemplo el trabajo de F1, o el de P o el de N... WF1, WF2, WP, WRoz, WN... son todas magnitudes -en principio-calculables. Pero si pregunto por el trabajo del cuerpo, o por el trabajo de una persona... esas preguntas no tienen sentido físico.
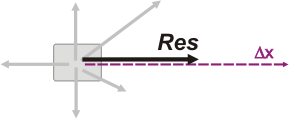
Incluso la resultante de todas las fuerzas que están actuando, si bien no se trata de una interacción en el sentido newtoniano de la palabra, no deja de ser una fuerza con todos los atributos de las fuerzas. Por lo tanto, bien podría preguntarme por el trabajo de la resultante... WRes también es -en principio- calculable. |
|
|
 |
|
|
| Como F . cos α es la componente de la fuerza que apunta en la dirección del desplazamiento (habitualmente llamada Fx) la definición podría escribirse así: |
|
|
| |
WF = Fx . Δx |
¡sólo para fuerzas constantes! |
|
|
|
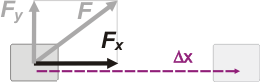
| Y cuya representación sería la siguiente: |
|
|
 |
|
|
Fijate que la definición ésta (que es totalmente equivalente a la primera) no considera el trabajo de la componente de F perpendicular al desplazamiento, Fy. Pero eso es absolutamente coherente con la definición inicial, ya que la perpendicular al desplazamiento forma con él un ángulo de 90°, y el coseno de 90° vale 0.
Una característica más: el trabajo es una magnitud que surge de un proceso. Un proceso que transcurre en cierto intervalo de tiempo, y en el que hay algún desplazamiento. No es una magnitud instantánea, como la velocidad, o la energía, o tantas otras que se definen para un instante de cierto sistema. Hay quienes lo dicen de este modo: el trabajo no es una función de estado.
Y la última. Es fácil demostrar (no voy a hacerlo) que el trabajo de la resultante es igual a la suma de los trabajos de cada una de las fuerzas que actúen sobre un cuerpo.
WRes = WF1 + WF2 + WF3 + ... + WFn
Esta propiedad casi pavota es utilísima, porque, como verás más en la siguiente lección existe un modo alternativo de averiguar el valor del trabajo de la resultante. |
|
|
CHISMES IMPORTANTES: |
|
|
- Si de fuerzas no constantes se tratara, el trabajo se puede calcular fraccionando los desplazamientos lo más que se pueda, para que en cada pequeña fracción el cambio en la fuerza sea despreciable. Luego, se suman todos los trabajos de todas las fracciones, y ya. Esa estrategia se puede simbolizar de esta manera:
WF = ∫ F dx cos α
El hecho de que el trabajo sea la suma integral del producto entre la fuerza y el diferencial de desplazamiento nos indica que otro modo de calcular trabajos será calculando áreas encerradas bajo la curva en gráficos F-x.
-
Un par de vectores se puede multiplicar de dos modos diferentes. El producto escalar es el modo que se utiliza para hallar el trabajo y otras magnitudes escalares. También está el producto vectorial, que es el otro modo, y cuando se utiliza, el resultado de la multiplicación es un vector. No es nuestro caso.
|
|
|
PREGUNTAS CAPCIOSAS: |
|

 |
- ¿Cuánto valdrá el trabajo de una fuerza perpendicular al desplazamiento?
- Si la definición de trabajo utiliza sólo los módulos de los vectores implicados, ¿de qué depende el signo de un trabajo?, ¿cuándo un trabajo es negativo?
- ¿Puede ser que erg (ergio), cal (caloría), eV (electrón volt) y l.atm (litro atmósfera) sean también unidades para trabajo? (Me quieren volver loco).
|
|
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jun-09. Buenos Aires, Argentina. |
|
|
|

