NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento oscilatorio armónico)
|
|

|
| |
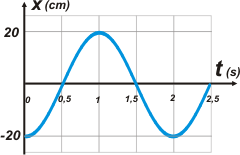
FIS (dN6.06)* - Un cuerpo de masa 200 g describe un movimiento oscilatorio armónico sobre una trayectoria horizontal siendo la representación gráfica de la posición en función del tiempo la que se muestra en la figura. |
a) Hallar el período del movimiento.
b) Calcular la frecuencia angular.
c) Escribir las ecuaciones horarias.
d) Representar gráficamente la velocidad y la aceleración en función del tiempo.
d) Calcular la velocidad y la aceleración máximas.
e) Calcular la constante del sistema.
f) Graficar la fuerza que actúa sobre el cuerpo e indicar su sentido. |
 |
|
|
|
| * Este ejercicio forma parte de la Guía de Ejercicios de Física 6to. Año Escuela de Comercio Carlos Pellegrini, UBA. |
|
|
El ejercicio es bien sencillo, casi de aplicación de fórmulas... pero alguna enseñanza interesante vamos a tratar de extraerle.
Lo primero que nos piden es hallar el período, T. Esa información se halla consignada en el gráfico que es parte del enunciado. Acordate que el período es el intervalo de tiempo entre dos posiciones idénticas (no solo en cuanto a la posición sino también al movimiento que realiza el cuerpo).
O sea, mirando el gráfico, un par de posiciones idénticas hay en 0 s y en 2 s, o también en 0,5 s y en 2,5 s. Y en varias más... Restando ambos pares te da lo mismo (obviamente), o cualquier otro par que hubieses elegido vos. |
|
|
|
|
|
Pero fijate que, por ejemplo, en 0,5 s y en 1,5 s también el cuerpo se halla en la misma posición (0 cm), pero no está realizando el mismo movimiento: en 0,5 s el cuerpo yendo hacia un lado y en 1,5 s está yendo hacia el lado contrario.
Pasemos al segundo ítem. Nos piden averiguar la frecuencia angular y es otra pavada, ya que -como ya recontra sabés- la frecuencia es la inversa del período:
f = 1 / T
f = 1 / 2 s
|
|
|
|
|
|
Ahora las ecuaciones.
Tenés que tener los modelos a mano y saber a qué querés llegar. Los modelos son éstos:
x = A cos (ωt+φ)
v = – A ω sen (ωt+φ)
a = – A ω² cos (ωt+φ)
En los que aparecen las mismas tres constantes en cada una: A, ω y φ.
A, la amplitud, es el apartamiento máximo y es un dato que figura en el grafico del enunciado. Miralo bien...
A = 20 cm
La pulsación, ω, podés obtenerla fácilmente a partir del período o la frecuencia, ya que:
ω = 2π . f
ω = 2π . 0,5 s-1
ω = π s-1
Y nos falta el ángulo de fase, φ. Para el ojo entrenado es obvio que φ es igual a π, porque la función coseno arranca de 1 o sea, el valor máximo. Y en el gráfico se ve que para el instante inicial (0 s) la función adopta su valor mínimo. La diferencia angular entre un máximo y un mínimo es justamente 180 grados, o sea π.
Pero si no te das cuenta de esto, podés usar la ecuación horaria de posición (ya está casi completa, solo falta φ) y le pedís que hable de alguna posisión y tiempo que surjan como dato del gráfico. Por ejempo en punto inicial, – 0,20 cm, que tiene en el instante 0 s. Y de ahí despejás φ.
– 20 cm = 20 cm . cos ( π s-1 . 0 s + φ )
– 1 = cos ( φ )
El coseno vale – 1 cuando el argumento vale π (eso es algo que te resonde la calculadora preguntando por la operación inversa del coseno [cos-1], que no debés confundir con la inversa multiplicativa, por eso te lo puse entre corchetes). De modo que:
φ = π
Ya tenemos las tres constantes, de modo que podemos escribir las ecuaciones horarias completitas: |
|
|
| |
x = 20 cm cos ( π s-1 t + π )
v = – 20π cm s-1 sen ( π s-1t + π )
a = – 20π2 cm s-2 cos ( π s-1t + π ) |
|
|
|
|
Calculemos primero la velocidad y aceleración máximas, vM y aM, ya que eso nos va a ayudar a graficar correctamente.
Tanto la función velocidad como la aceleración tendrán su máximos cuando el seno y el coseno valgan 1 que es el máximos de esas funciones. Y como recordamos que 1 es multiplicativamente neutro, podemos ignorar esa parte de cada ecuanción y nos queda: |
|
|
| |
vM = 20π cm/s
aM = 20π² cm/s² |
|
|
|
|
| Habrás notado que tomé el valor absoluto, que es lo correcto. Vamos, ahora sí, a los gráficos: |
|
|
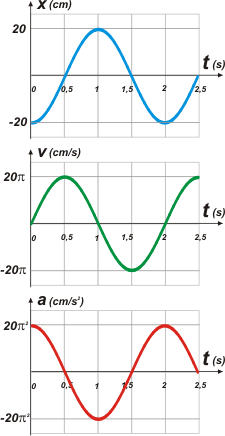
Verás que, como siempre, graficamos en tandem, o sea, encolumnados con una misma escala de tiempo y en el mismo orden: posición, velocidad y aceleración.
Las escalas verticales no tienen ninguna importancia ya que representan magnitudes diferentes.
Aprovechá para discutir los sentidos de cada magnitud vectorial. Por ejemplo... mirá el instante 1 s (lo elegí porque es bastante parecido al punto más alto en un tiro vertical de un cuerpo que arrojás hacia arriba y después de subir empieza a bajar, y en el que tomamos un sistema de referencia positivo hacia arriba). En la altura máxima la velocidad vale cero, y la aceleración es -g.
Acá no se trata de altura sino de oscilaciones del cuerpo... pero el parecido es bastante grande.
Estudiá vos qué pasa en otros instantes. |
 |
|
|
|
Para obtener la constante elástica del sistema tenés que imaginar que el cuerpo oscila unido a un resorte de constante, k (esa es la constante del sistema), y luego basta con recordar que k se halla relacionada con la pulsación:
ω² = k / m
De donde
k = ω² . m
k = π² s-2 . 200 g
k = π² s-2 . 0,2 kg
|
|
|
|
|
|
Y nos queda el gráfico de fuerza, pero te lo voy a dejar a vos. El gráfico de fuerza es similar al de aceleración a excepción de la escala vertical ya que mide diferente magnitud y unidad. Pero cualitativamente es idéntico ya que la fuerza que hace oscilar al cuerpo debe ser la resultante, de modo que:
F = m . a
Que oscilará igual que el de aceleración, pero entre los valores m.a y -m.a. |
|
|
| |
|
 |
| DESAFIOS: ¿En qué cambiarían los gráficos si φ valiese 3π? |
|
| Algunos derechos reservados con anticipación.
Se permite su reproducción citando la fuente. Última actualización dic-18. Buenos Aires, Argentina. |
|
|
|

