NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
|
|

|
 |
5.05 - Un móvil que está enganchado a un resorte
de constante elástica 9.475 N/m recorre una circunferencia
en un plano horizontal a razón de 20
vueltas por segundo. Si la masa del cuerpo es de
200 g y la longitud natural del resorte es de
20 cm, el radio de la circunferencia es de: |
|
a) 30 cm b) 10 cm c) 25 cm
d) 45 cm e) ninguno de ellos
|
No te asustes por el esquema de acá abajo... parece un poco complicado... ya lo sé... pero dejame que te lo explique... |
|
|
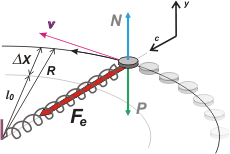 |
En el centro aparece el móvil -que lo hice como una especie de tejo, de moneda, o algo así- y gira en un plano horizontal (guarda, que yo hice un dibujo en perspectiva) en sentido antihorario, ¿te cierra?
Bueno, el tejo gira gracias a que un resorte tira de él hacia el centro de la circunferencia de giro.
Si no fuera por esa fuerza que tira hacia adentro, el tejo saldría despedido con esa velocidad tangencial, v, que le representé en rosa. |
|
|
Ahora bien... el resorte, para poder hacer esa fuerza que tan bien le viene al tejo, tiene que estar estirado (es la única manera de que un resorte haga una fuerza hacia adentro). De modo que la circunferencia que describe el tejo en su movimiento circular es igual a la longitud natural del resorte, más el estiramiento necesario para hacer la fuerza.
R = lo + Δx
Ahora estamos en condiciones de empezar a resolver el ejercicio. En el eje vertical no hay problemas:
N + P = 0
En el eje radial, en cambio, acá está la papa:
Fe = m . ac
k Δx = m . 4π² . ƒ² . R
El estiramiento del resorte se puede expresar en función del Radio de la circunferencia (la longitud actual del resorte): Δx = R — lo |
|
k ( R — lo) = m . 4π² . ƒ² . R
k . R — k . lo = m . 4π² . ƒ² . R
k . R — m . 4π² . ƒ² . R = k . lo
R ( k — m . 4π² . ƒ²) = k . lo
R = k . lo / ( k — m . 4π² . ƒ² )
|
|
|
|
R = 9.475 N/m . 0,2 m / ( 9.475 N/m — 0,2 kg. 4π² . 400 s-² )
|
|
|
|
Discusión: Te propongo este ejercicio de imaginación, a ver si te sale. Si quisiéramos que el cuerpo girase más rápido, el resorte tendría que hacer más fuerza, ¿no es cierto? De modo que el radio de giro aumenta porque el resorte, para hacer más fuerza, tiene que estar más estirado.
Desafío: ¿Cuál es la menor frecuencia a la que puede girar este mismo cuerpo con este mismo resorte? |
 |
| |
| |
| Algunos derechos reservados.
Este material didáctico no puede ser comercializado... Pero podés leerlo, memorizarlo, olvidarlo, imprimirlo, copiarlo, prestarlo, compartirlo, regalarlo, atesorarlo, y muchas cosas más. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

