NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
 |
NMS 4.22 - En junio de 2015 el salélite de la NASA Deep Space Climate Observatory (DSCOVR) fue colocado en órbita de la Tierra y del Sol simultáneamente. Esa posición extraordinaria recibe el nombre de lagrangiano 1, L1, debido a que en 1772, el matemático italofrancés Joseph-Louis Lagrange predijo la existencia de ésta y cuatro posiciones más (L2, L3, L4 y L5) con la misma propiedad en todo sistema planetario.
Sabiendo que la distancia Tierra-Sol es de 150 millones de kilómetros, que el satélite se halla alineado con el Sol y a 1,4 millones de kilómetros de la Tierra verificar que el período del satélite es igual al período de rotación de la Tierra al Sol.
La masa de la Tierra MT = 6 x1024 kg, y la del Sol MS = 2 x1030 kg. |
|
|
Empecemos con un esquema que nos aclare el asunto y nos sirva para denominar las magnitudes con las que vamos a trabajar. (Esquema fuera de escala). |
|
|
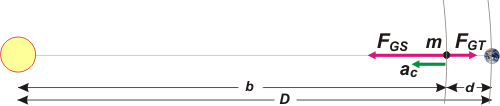 |
Llamaremos D a la distancia Tierra-Sol, d es la distancia desde el satélite hasta el centro de la Tierra y b es la distancia desde el satélite hasta el Sol; no se nos escapará que d + b = D.
FGT es la fuerza gravitatoria entre el objeto y la Tierra, FGS es la fuerza gravitatoria entre el objeto y al Sol, MT la masa de la Tierra, MS la del Sol y m la del satélite. En el esquema metí el DCL del satélite. Comprenderás que la fuerza centrípeta sea mayor que la centrífuga, dado que el satélite obedece la 2da. Ley de Newton y la aceleración del satélite tiene que ser centrípeta.
FGS — FGT = m ac
Donde ac es la aceleración centrípeta del satélite. Y...
FGS = G . MS . m / b²
FGT = G . MT . m / d²
ac = 4 π² b / T²
Y donde T es el período de giro del satélite que debemos verificar que vale lo mismo que el de la Tierra. |
| |
G . MS . m |
— |
G . MT . m |
= |
m 4 π² b |
|
|
|
|
|
| b² |
d² |
T² |
|
|
|
La masa del satélite, m, aparece en los dos miembros multiplicando, vuela ya mismo: |
|
|
| |
G . MS |
— |
G . MT . |
= |
4 π² b |
|
|
|
|
|
| b² |
d² |
T² |
|
|
|
Calculamos esos cocientes, despejamos T y lo calculamos: |
|
|
| |
T = 3,17 x 107 s |
o sea, 1 año (más o menos) |
|
|
|
También podríamos hacer una demostración general (sin cálculos numéricos), pero no es sencillo y excede el nivel de dificultad de un curso de educación media. |
|
|
 |
|
Para estar siempre alineado con el Sol el satélite debe girar con el mismo período de la Tierra, o sea, un año.
La NASA ofrece libremente alrededor de 12 fotografías diarias de la Tierra tomadas desde el satélite con su equipo fotográfico EPIC. Pueden verse en este sitio: https://epic.gsfc.nasa.gov/
Acá una de las fotografías más imponentes: un tránsito de la Luna frente a la Tierra, o sea, un día de eclipse solar, o sea, los cuatro cuerpos alineados casi perfectamente.
Sobrecogedora. |
|
|
| |
|
|
| |
|
 |
| DESAFIO: ¿Dónde orbita el DSCOVR, en el plano ecuatorial o en el plano de la eclíptica? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente, o sea: de dónde está afanado. Última actualización oct-17. Buenos Aires, Argentina. |
|
|
|

