NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Materia oscura - Gravitación)
|
|

|
NMS 4.18 - Calcular la cantidad de materia oscura y materia visible en nuestra galaxia a partir de la velocidad de traslación de sus estrellas según el gráfico adjunto*.
|
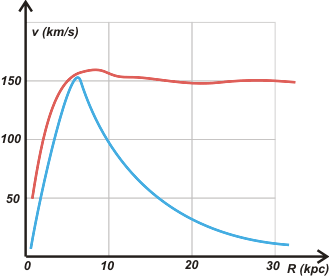 |
En rojo se muestra la velocidad medida en km/s en función de la distancia al centro de la galaxia (R) en kiloparsecs (1 kpc equivale a 3.262 años luz).
En azul se esquematiza la velocidad teórica calculada en base a la acción gravitatoria de la masa visible.
Es evidente que al aumentar la distancia al centro de la galaxia, la velocidad debería disminuir, pero en cambio permanece casi constante.
Esto se explica con la presencia de una gran masa adicional denominada "materia oscura". |
|
|
|
¡Qué ejercicio tan interesante! ¡Mientras lo hacemos podemos sentirnos cosmólogos modernos! ¡Y descubrir la materia oscura!
A ver si entendemos el asunto: la Vía Láctea, nuestra galaxia, funciona básicamente igual que un sistema planetario. Es así: la masa central del sistema planetario, el Sol, atrae gravitatoriamente a los planetas y los hace girar en torno a él, cada uno a su velocidad. Cuanto más cerca más rápido y cuanto más lejos más lento. Miremos cómo se relacionan esas dos magnitudes, lejanía y velocidad: |
|
|
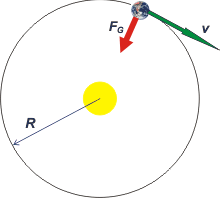 |
Tomemos como ejemplo nuestro planeta. Sobre él actua la fuerza gravitatoria, FG, con que lo atrae el Sol, que se encuentra a una distancia R y le produce una velocidad v.
De más está decir que el movimiento de la Tierra se describe con una aceleración centrípeta, ac, que es igual a:
ac = v² / R
Escribamos la 2da. ley de la dinámica y la de gravitación universal: |
|
|
|
FG = mT . ac
FG = G . mT . MS / R²
Donde MS y mT son la masa del Sol y de la Tierra respectivamente.
Las podemos igualar (hablan de la misma fuerza). |
|
|
| |
mT . v² |
= |
G . mT . MS |
|
|
|
| R |
R² |
|
|
|
| Y también podemos cancelar la masa de la Tierra y una vez el radio de órbita: |
|
|
|
|
|
Y acá podés ver que si aumenta el radio de órbita disminuye (cuadráticamente) la velocidad de desplazamiento. Y eso, además, no depende del planeta que se trate. Podés concluir con mucha tranquilidad que Júpiter o Plutón deben desplazarse alrededor del Sol mucho más lento que la Tierra.
En una galaxia cualquiera pasa lo mismo. Las estrellas cercanas al centro deben moverse más rápido y las periféricas mucho más lento. Tal vez quieras objetar que una galaxia no tiene un cuerpo central al estilo del Sol, una super estrella o un agujero negro. Bueno, tal vez los tenga, pero eso no importa ya que la masa se comporta como si estuviese toda reunida en un punto central sin importar su distribución ni lejanía. |
|
|
 |
|
Materia visible no es sólo la que podemos ver con los ojos. Los telescopios pueden ver en longitudes de onda que para nuestros ojos son invisibles. |
La única diferencia es que como son las mismas estrellas las que forman la galaxia, y le dan su masa, una estrella cualquiera es atraída centralmente sólo por la masa reunida en una esfera teórica cuyo radio es igual a la distancia entre la estrella y el centro de la galaxia. De modo que la gráfica teórica de velocidad en función de la distancia al centro es la que se muestra en azul en el gráfico del ejercicio.
Pero para una estrella periférica (esto es lo que importa para resolver este ejercicio), como el Sol, la cosa funciona como si toda la masa de la galaxia, MG, estuviese reunida en su núcleo. Eso nos permite calcular la masa de una galaxia usando la fórmula que obtuvimos con las ecuaciones de Newton. |
|
|
|
|
|
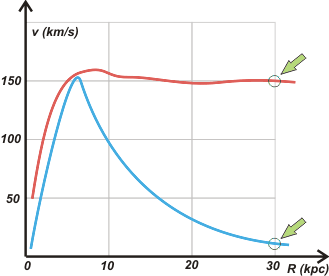
La curva teórica (azul) fue calculada suponiendo que la masa de la galaxia se obtiene sumando la masa de todas las estrellas que observamos. A esa masa teórica podemos llamarla masa de la galaxia luminosa (que podemos "ver"), MGL. En cambio la curva roja se construyó midiendo directamente las velocidades de cientos de estrellas de la galaxia, que responden a la gravitación de la masa real de la galaxia, MGR.
Tomando la distancia y las velocidades (teórica, vT, y real, vR) de una estrella periférica (flechas) podemos calcular eso dos valores de masa galáctica. |
|
|
 |
|
|
Acordate que 1 kpc es igual a 3.262 años luz. Y que 1 año luz es igual a 9,46.1015 m.
Por lo tanto:
1 kpc = 3,1.1019 m
Y tomaremos una distancia al centro de la galaxia de 30 kpc. Y aproximadamente las velocidad valdrán:
vT = 1,5.104 m/s
vR = 1,5.105 m/s
|
|
|
|
| MGL = |
|
(1,5 .104 m/s)2 . 9,3.1020 m |
= 3,1 1039 kg |
|
| (6,67.10-11 Nm²/kg²) |
|
|
|
| MGR = |
|
(1,5 .105 m/s)2 . 9,3.1020 m |
= 3,1 1041 kg |
|
| (6,67.10-11 Nm²/kg²) |
|
|
|
| ¡En la galaxia parece haber 100 veces más materia de la que podemos ver! Y a ese exceso de materia la llamamos materia oscura. Resulta muy interesante que todas las galaxias espirales que se han estudiado revelan el mismo comportamiento que la nuestra. Parece ser que la materia oscura es mayoritaria en el universo. |
|
|
| |
MGL = 3,1 1039 kg , MGR = 3,1 1041 kg |
|
|
|
|
|
|
|
| * Este sencillo y sorprendente ejercicio me fue acercado por Maria Celeste Artale, y el gráfico fue construido a partir de la información volcada en el sitio de Sergio A Cellone en el que se puede encontrar más información sobre este fenómeno. |
|
|
|
| DESAFIO: ¿Y qué será la energía oscura? |
|
 |
| Algunos derechos reservados.
Se permite tu reproducción recitando en la fuente. Última actualización oct-15. Buenos Aires, Argentina. |
|
|
|

