NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Gravitación)
|
|

|
NMS d4.03- Suponiendo que el campo gravitatorio a
nivel del mar tiene una intensidad de 9,8 m/s²,
cuál será su intensidad en el Aconcagua, a
6.000 m de altura. Expresarla en porcentaje.
Radio terrestre = 6.360 km.
La aceleración de la gravedad, g, es la que adquiere un cuerpo cualquiera cuando sobre él actúa una sola fuerza, la fuerza gravitatoria, que en las cercanías de la superficie terrestre recibe el nombre de peso. En una caída libre, por ejemplo.
Tomemos ése ejemplo, que es el más sencillo: el de la caída libre. El peso -lo acabo de decir- no es otra que la fuerza gravitatoria; entonces podemos decir que para un cuerpo de masa m que está cayendo libremente acá en esta habitación (no me digas que estás leyendo esto en una nave espacial porque me pego un tiro en #%$"@ª#) se cumplen dos cosas: por un lado la ley de la masa:
|
ΣF = m . a
Hay una sola fuerza actuando, el peso; y la aceleración es justamente esa que llamamos g:
P = m . g
Y por otro lado la ley de gravitación universal, que nos revela parte de la naturaleza de la fuerza gravitatoria, de la fuerza peso:
P = G . m . M / RT²
Donde G es una constante de proporcionalidad, m la masa del cuerpo que está cayendo, M es la masa de la Tierra y RT su radio, o sea la distancia entre los centros de masa de los cuerpos que se están atrayendo, Tierra y el cuerpo que cae.
Como se trata de la misma fuerza puedo igualar los segundos miembros, y queda:
m . g = G . m . M / RT²
|
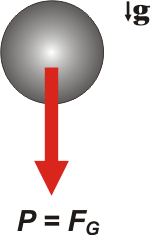
| El DCL nos muestra la única fuerza que actúa durante una caída libre: la fuerza con que la Tierra atrae a todos los cuerpos que se hallan en su proximidad, y que llamamos vulgarmente: peso. |
|
 |
|
|
|
Ahora podemos cancelar la masa del cuerpo en caída libre (lo cual no es ninguna trivialidad, y eso te lo cuento abajo en la discusión) y queda:
g = G M / RT²
que resumidamente nos dice cómo calcular la aceleración de caída libre para cualquier lugar del universo. |
|
 |
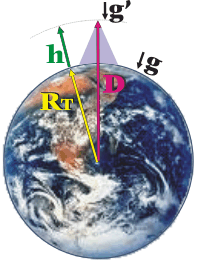
Si aplicamos esa misma relación para averiguar con qué aceleración caería al suelo un cuerpo en la cima del Aconcagua
g' = G . M / D²
donde D es esa distancia al centro de la Tierra, o sea un radio terrestre más la altura del aconcagua.
Si dividimos g'/g, obtendremos la relación que nos pìde el enunciado del ejercicio... de modo que habrá que hacer:
g'/g = G M RT²/ G M D²
g'/g = RT²/ D²
g'/g = (6.360 km)²/ (6.366 km)² |
 |
|
|
|
|
|
¿Querés dicutir conmigo sobre el CBC? |
| O sea, que el lugar de caer con una aceleración de 9,80 m/s², en la cima del Aconcagua, los cuerpos caen con una aceleración de 9,78 m/s²... qué terrible. |
|
|
| |
|
|
DISCUSION: Aunque vos no lo creas, esa operación tonta que hicimos, de cancelar la masa del cuerpo nos está diciendo que cualquier cuerpo, independientemente de su masa, va a caer con la misma aceleración que otro (siempre y cuando se halle en el mismo lugar). Esa fue una de las cruzadas de Galileo, que, como no podía demostrarlo analíticamente, propuso corroborarlo experimentalmente arrojando sus bolas desde la terraza de la torre inclinada de Pisa. El experimento no se hizo y hubo que esperar otros 50 años para que apareciera Newton con su Ley... que le dio la razón a Galileo.
Pero la historia no termina ahí, resulta que Einstein se puso a mirar la ecuación detenidamente y había algo que no le cerraba, que le molestaba. Hasta que se dio cuenta. Resulta que la masa de la ecuación de la segunda ley, y la masa de la ecuación gravitatoria ¡no eran la misma masa! Eran del mismo cuerpo, sí... pero representaban propiedades diferentes.
La masa que usó Newton para su segunda Ley (ΣF = m a) es una medida de cuánto se resiste un cuerpo a que le cambien su estado de velocidad. En cambio las masas que usa en la Teoría de Gravitación (F = G . m . m' / d²) son una medida de la propiedad de los cuerpos de ser atraídos gravitatoriamente. Todo el mundo daba por sentado que eran lo mismo, pero Einstein nos convenció de que no había ninguna ley en el universo que indicara que tenian que valer igual ni -menos que menos- ser la misma cosa.
Para diferenciarlas, las llamó masa inercial a la que aparece en la 2da Ley, y masa gravitatoria la otra. Pero, convencido de que funcionaban de manera idéntica Einstein le puso nombre a esta curiosidad: principio de equivalencia (entre ambos tipos de masa), y constituye uno de los pilares de la Teoría de la Relatividad General. Tomá mate. |
|
 |
| DESAFIO: Averiguar cómo varía la aceleración de la gravedad a lo largo de un túnel excavado en la Tierra. (Mirá: lo dejé pensando...) |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-08. Buenos Aires, Argentina, América, Planeta Tierra, Sistema Solar, Galaxia Via Láctea, Universo. |
|
|
|

