NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(dinámica de las rotaciones)
|
|

|
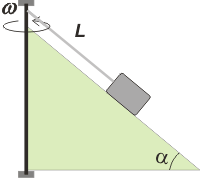
| NMS dN3.24 - Un plano inclinado gira con una velocidad
angular constante “ω” y sobre el se encuentra
un bloque de masa “m” atado a una cuerda de largo “L” como se muestra en la
figura. Determinar la velocidad “ω” en el instante
en que el cuerpo se desprende del plano. |
 |
|
¡No te vayas, no te vayas! ¡Creeme, es un ejercicio muy sencillo! Ya sé que esa imagen asusta... pero creeme, no sólo es un ejercicio sencillo sino que tiene una enseñanza muy significativa. ¡No te la pierdas!
Buenísimo, te quedaste. La enseñanza viene al principio. Prestá atención. Por supuesto, como en todo ejercicio de dinámica tenemos que arrancar con un DCL, pero... |
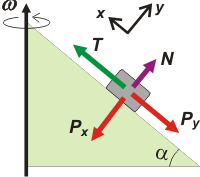 |
Si vos ves un plano inclinado la costumbre te hace dibujar algo así, ¿no es cierto?
Si además ya tenés una buena cantidad de horas de vuelo tal vez hayas dibujado algo parecido, pero sin la fuerza de apoyo, N, ya que el enunciado plantea la situación en la que el cuerpo se separa del plano, y eso es -justamente- cuando el apoyo se hace cero. |
|
|
|
Pero en cualquiera de los dos casos habrás desacertado. No está del todo mal, pero ahí se te arma un problema dinámico y algebraico del que no sé si salís.
La clave es ésta: en todos los ejercicios de rotaciones siempre te conviene elegir un sistema de referencia cuyo eje coincida con el radio de rotación del cuerpo. El DCL adecuado es éste: |
|
|
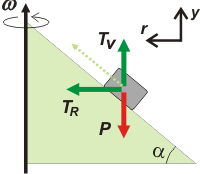 |
Y la única fuerza que tenés que descomponer es la tensión que hace la cuerda.
Entonces tenemos: tensión en la dirección vertical, TV; tensión en la dirección radial o centrípeta, TR; y el peso, P.
Como ves, no dibujé el apoyo, por el motivo que mencioné más arriba.
Vas a ver que con este sistema de referencia el ejercicio es muy sencillo. |
|
|
|
Las ecuaciones de Newton para el eje vertical y centrípeto son:
ΣFy = 0 → TV — P = 0 → TV = m . g [1]
ΣFc = m ac → TR = m ac → TR = m ω² . R [2]
Ahora un poco de geometría y de álgebra (nada que no hayas hecho ya antes). Las componentes de T valen...
TV = T sen α
TR = T cos α
|
|
|
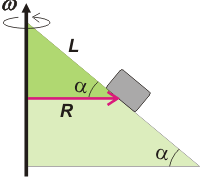 |
Por otro lado, si mirás bien el triángulo que acabo de sombrearte, acordarás conmigo que el radio de giro, R, es igual a:
R = L cos α
(No te olvides de considerar que tratamos con "cuerpos puntuales").
Ahora si metemos estas tres relaciones geométricas en las dos ecuaciones anteriores, el ejercicio sale con fritas. Acá va: |
|
|
|
T sen α = m . g
T cos α = m ω² . L cos α
De la primera despejamos T y lo que da lo metemos en la segunda, en la que previamente cancelamos ese coseno que está multiplicando en los dos miembros.
m . g / sen α = m ω² . L
Cancelo las masas y despejo la velocidad angular.
ω² = g / L . sen α
|
|
|
|
|
|
No hace falta que te diga que la potencia ½ es lo mismo que raíz cuadrada.
No puedo dejar de decirte que si te emperrás en resolver el ejercicio mirándolo desde un SR paralelo y perpendicular al plano, como te muestro al principio, el ejercicio igual debe salir, y tenés que arribar al mismo resultado. Simplemente te va a dar un poco (bastante) más de trabajo. |
|
|
| |
|
|
| DESAFIO: ¿Te animás a resolverlo con el SR inadecuado? |
|
 |
| Algunos derechos reservados.
Me envió este ejercicio mi colega José Velásquez. Se permite tu reproducción recitando en la fuente. Última actualización dic-12. Buenos Aires, Argentina. |
|
|
|

